题目内容
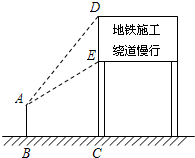 某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°.求路况指示牌DE的高度.(精确到0.01米)
某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°.求路况指示牌DE的高度.(精确到0.01米)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点A作AF⊥DC于点F,在Rt△ADF中求出DF,在Rt△AEF中求出EF,继而根据DE=DF-EF,可得出答案.
解答:解:过点A作AF⊥DC于点F,

在Rt△ADF中,AF=3.2m,tan∠DAF=tan52°=
,
则DF=AFtan52°=3.2×1.28≈4.10米.
在Rt△AEF中,AF=3.2m,tan∠EAF=tan32°=
,
则DF=AFtan32°=3.2×0.62≈2.00米.
故可得DE=DF-EF=2.10米.
答:路况指示牌DE的高度为2.10米.

在Rt△ADF中,AF=3.2m,tan∠DAF=tan52°=
| DF |
| AF |
则DF=AFtan52°=3.2×1.28≈4.10米.
在Rt△AEF中,AF=3.2m,tan∠EAF=tan32°=
| EF |
| AF |
则DF=AFtan32°=3.2×0.62≈2.00米.
故可得DE=DF-EF=2.10米.
答:路况指示牌DE的高度为2.10米.
点评:本题考查了解直角三角形的应用,要求学生能借助仰角构造直角三角形并解直角三角形,难度一般.

练习册系列答案
相关题目
若分式
在实数范围内有意义,则x的取值范围为( )
| 1 |
| x+2 |
| A、x>2 | B、x>-2 |
| C、x≠2 | D、x≠-2 |

 在我市中小学生“人人会乐器”演奏比赛中,某班10名学生成绩统计如图所示,则这10名学生成绩的中位数是
在我市中小学生“人人会乐器”演奏比赛中,某班10名学生成绩统计如图所示,则这10名学生成绩的中位数是
 一枚质地均匀的正方体骰子六个面上标有数字1、2、3、4、5、6.随机抛掷这枚骰子一次,把着地一面的数字记做P点的横坐标,将该数的3倍记做P点的纵坐标.如图,抛物线y=-x2+4x+5与x轴负半轴交于点A,点B(4,5)在该抛物线上,则点P落在抛物线与直线AB围成的区域内(阴影部分,含边界)的概率是
一枚质地均匀的正方体骰子六个面上标有数字1、2、3、4、5、6.随机抛掷这枚骰子一次,把着地一面的数字记做P点的横坐标,将该数的3倍记做P点的纵坐标.如图,抛物线y=-x2+4x+5与x轴负半轴交于点A,点B(4,5)在该抛物线上,则点P落在抛物线与直线AB围成的区域内(阴影部分,含边界)的概率是 同学们,你认识如图所示的卡通人物吗?没错,它就是美国著名3D卡通电影《里约大冒险》(Rio)中的两个主人公:两只漂亮的鹦鹉--布鲁和珠儿,凭借着影片中所寄寓的独特情感,该片在
同学们,你认识如图所示的卡通人物吗?没错,它就是美国著名3D卡通电影《里约大冒险》(Rio)中的两个主人公:两只漂亮的鹦鹉--布鲁和珠儿,凭借着影片中所寄寓的独特情感,该片在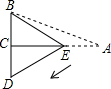 如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=
如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=