题目内容
 如图,在矩形ABCD中,点M、N在线段AD上,∠MBC=∠NCB=60°,点E、F分别为线段CN、BC上的点,连接EF并延长,交MB的延长线于点G,EF=FG.
如图,在矩形ABCD中,点M、N在线段AD上,∠MBC=∠NCB=60°,点E、F分别为线段CN、BC上的点,连接EF并延长,交MB的延长线于点G,EF=FG.(1)点K为线BM的中点,若线段AK=2,MN=3,求矩形ABCD的面积;
(2)求证:MB=NE+BG.
考点:矩形的性质,全等三角形的判定与性质,勾股定理
专题:几何综合题
分析:(1)根据直角三角形斜边上的中线等于斜边的一半求出BM,再利用勾股定理列式求出AB的长,然后利用∠NCD的正切值求出DN的长,再求出AD,再根据矩形的面积公式列式计算即可得解;
(2)过点G作GH∥NC交CB的延长于点H,先利用“边角边”证明△ABM和△DCN全等,根据全等三角形对应边相等可得BM=CN,再根据两直线平行,内错角相等求出∠H=∠ECF=60°,然后利用“角边角”证明△FHG和△FCE全等,根据全等三角形对应边相等可得HG=CE,再求出△BHG是等边三角形,根据等边三角形的三条边都相等可得BG=HG,从而得证.
(2)过点G作GH∥NC交CB的延长于点H,先利用“边角边”证明△ABM和△DCN全等,根据全等三角形对应边相等可得BM=CN,再根据两直线平行,内错角相等求出∠H=∠ECF=60°,然后利用“角边角”证明△FHG和△FCE全等,根据全等三角形对应边相等可得HG=CE,再求出△BHG是等边三角形,根据等边三角形的三条边都相等可得BG=HG,从而得证.
解答:(1)解:∵矩形ABCD,
∴AD=BC,AB=CD,
在Rt△ABM中,∵点K为斜边BM中点,
∴BM=2AK=4,
∵∠MBC=60°,
∴∠ABM=30°,
∴AM=
BM=2,AB=
=
=2
,
在△CDN中,∵∠NCB=60°,
∴∠NCD=30°,
∴DN=
=
=2,
∴AD=2+3+2=7,
∴矩形ABCD的面积是:2
×7=14
;
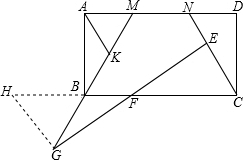
(2)证明:过点G作GH∥NC交CB的延长于点H,
∵在△ABM和△DCN中,
,
∴△ABM≌△DCN(SAS),
∴BM=CN,
∵GH∥NC,
∴∠H=∠ECF=60°,
∵在△FHG和△FCE中,
,
∴△FHG≌△FCE(ASA),
∴HG=CE,
在△BHG中,∠HBG=∠MBC=60°=∠H,
∴△BHG是等边三角形,
∴BG=HG=EC,
∴BM=CN=NE+CE=NE+BG
∴AD=BC,AB=CD,
在Rt△ABM中,∵点K为斜边BM中点,
∴BM=2AK=4,
∵∠MBC=60°,
∴∠ABM=30°,
∴AM=
| 1 |
| 2 |
| BM2-AM2 |
| 42-22 |
| 3 |
在△CDN中,∵∠NCB=60°,
∴∠NCD=30°,
∴DN=
| CD | ||
|
2
| ||
|
∴AD=2+3+2=7,
∴矩形ABCD的面积是:2
| 3 |
| 3 |

(2)证明:过点G作GH∥NC交CB的延长于点H,
∵在△ABM和△DCN中,
|
∴△ABM≌△DCN(SAS),
∴BM=CN,
∵GH∥NC,
∴∠H=∠ECF=60°,
∵在△FHG和△FCE中,
|
∴△FHG≌△FCE(ASA),
∴HG=CE,
在△BHG中,∠HBG=∠MBC=60°=∠H,
∴△BHG是等边三角形,
∴BG=HG=EC,
∴BM=CN=NE+CE=NE+BG
点评:本题考查了矩形的性质,直角三角形斜边上的中线等于斜边的一半的性质,全等三角形的判定与性质,解直角三角形,综合题,但难度不大,仔细分析图形并熟记各性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若分式
在实数范围内有意义,则x的取值范围为( )
| 1 |
| x+2 |
| A、x>2 | B、x>-2 |
| C、x≠2 | D、x≠-2 |
下列事件是随机事件的是( )
| A、通常加热到100℃时,水沸腾 |
| B、篮球队员在罚球线上投篮一次,未投中 |
| C、度量三角形内角和,结果是360° |
| D、掷一个质地均匀的正方体骰子,向上的一面出现的点数大于0 |
 在我市中小学生“人人会乐器”演奏比赛中,某班10名学生成绩统计如图所示,则这10名学生成绩的中位数是
在我市中小学生“人人会乐器”演奏比赛中,某班10名学生成绩统计如图所示,则这10名学生成绩的中位数是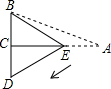 如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=
如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=