题目内容
骨牌的形状有三种：边长为1的等边三角形，由两个边长为1的等边三角形形成的菱形和由3个边长为1的等边三角形所拼成的梯形．一副骨牌有222块菱形，333块等边三角形，444块梯形．是否能用这些骨牌 拼成一个周长为888的多边形．（在拼接时，骨牌与骨牌之间不能留有空隙）
考点：奇数与偶数
专题：
分析：根据所有骨牌的周长之和为奇数，得出如果能够用所有这些骨牌拼成一个周长为888的多边形的话，那么，所有的骨牌的周长之和就应当等于多边形的周长加上各个骨牌的公共边界的长度之和的2倍，从而为偶数，导致矛盾，即可得出答案．
解答：解：∵边长为1的等边三角形，由两个边长为1的等边三角形形成的菱形和由3个边长为1的等边三角形所拼成的梯形，
且一副骨牌有222块菱形，333块等边三角形，444块梯形，
∴所有骨牌的周长之和为奇数，
所以，如果能够用所有这些骨牌拼成一个周长为888的多边形的话，
那么，所有的骨牌的周长之和就应当等于多边形的周长加上各个骨牌的公共边界的长度之和的2倍，从而为偶数，导致矛盾．
故不能用这些骨牌 拼成一个周长为888的多边形．
且一副骨牌有222块菱形，333块等边三角形，444块梯形，
∴所有骨牌的周长之和为奇数，
所以，如果能够用所有这些骨牌拼成一个周长为888的多边形的话，
那么，所有的骨牌的周长之和就应当等于多边形的周长加上各个骨牌的公共边界的长度之和的2倍，从而为偶数，导致矛盾．
故不能用这些骨牌 拼成一个周长为888的多边形．
点评：此题主要考查了奇数和偶数，根据奇数与偶数的性质得出所有的骨牌的周长之和为奇数进而求出是解题关键．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
同学们，你认识如图所示的卡通人物吗？没错，它就是美国著名3D卡通电影《里约大冒险》（Rio）中的两个主人公：两只漂亮的鹦鹉--布鲁和珠儿，凭借着影片中所寄寓的独特情感，该片在下列事件是随机事件的是（ ）
| A、通常加热到100℃时，水沸腾 |
| B、篮球队员在罚球线上投篮一次，未投中 |
| C、度量三角形内角和，结果是360° |
| D、掷一个质地均匀的正方体骰子，向上的一面出现的点数大于0 |
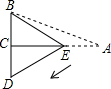如图，在三角形纸片ABC中，∠BCA=90°，∠BAC=30°，AC=3| 3 |
| A、2 | ||
| B、3 | ||
C、2
| ||
D、
|
下列事件是必然事件的是（ ）
| A、随机掷一枚质地均匀的硬币，正面朝上 |
| B、三角形的内角和等于180° |
| C、买100张中奖率为1%的彩票一定会中奖 |
| D、两个数相加，和大于零 |