题目内容
在△ABC中,∠A是钝角,H是垂心,AH=BC,则∠BHC=( )
| A、30° | B、45° |
| C、60° | D、75° |
考点:三角形的五心
专题:计算题
分析:先画出几何图形,易得∠AEH=90°,∠ADB=90°,根据等角的余角相等得到∠1=∠2,根据“AAS”可判断△HAE≌△BCE,则HE=BE,于是得到△HEB为等腰直角三角形,根据等腰直角三角形的性质得到∠BHC=45°.
解答:解:如图, AD、CE、BF为△ABC的高,H点为三条高线的交点,即H是垂心,
AD、CE、BF为△ABC的高,H点为三条高线的交点,即H是垂心,
∵AD、CE为△ABC的高,
∴∠AEH=90°,∠ADB=90°,
∴∠1=∠2,
∵在△HAE和△BCE中
,
∴△HAE≌△BCE(AAS),
∴HE=BE,
∴△HEB为等腰直角三角形,
∴∠BHC=45°.
故选B.
 AD、CE、BF为△ABC的高,H点为三条高线的交点,即H是垂心,
AD、CE、BF为△ABC的高,H点为三条高线的交点,即H是垂心,∵AD、CE为△ABC的高,
∴∠AEH=90°,∠ADB=90°,
∴∠1=∠2,
∵在△HAE和△BCE中
|
∴△HAE≌△BCE(AAS),
∴HE=BE,
∴△HEB为等腰直角三角形,
∴∠BHC=45°.
故选B.
点评:本题考查了三角形的五心:三角形的内心、外心、重心、垂心和旁心.

练习册系列答案
相关题目
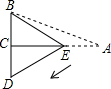 如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=3
如图,在三角形纸片ABC中,∠BCA=90°,∠BAC=30°,AC=3| 3 |
| A、2 | ||
| B、3 | ||
C、2
| ||
D、
|
为了解某区九年级学生课外体育活动的情况,从该年级学生中随机抽取了4%的学生,对其参加的体育活动项目进行了调查,将调查的数据进行统计并绘制了扇形图和条形图.下列结论错误的是( )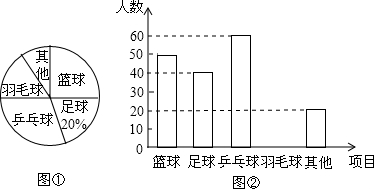

| A、被抽测学生中参加其他体育项目活动人数占10% |
| B、被抽测学生中参加羽毛球项目人数为30人 |
| C、估计全区九年级参加篮球项目的学生比参加足球项目的学生多20% |
| D、全区九年级大约有1500名学生参加乒乓球项目 |
 一枚质地均匀的正方体骰子六个面上标有数字1、2、3、4、5、6.随机抛掷这枚骰子一次,把着地一面的数字记做P点的横坐标,将该数的3倍记做P点的纵坐标.如图,抛物线y=-x2+4x+5与x轴负半轴交于点A,点B(4,5)在该抛物线上,则点P落在抛物线与直线AB围成的区域内(阴影部分,含边界)的概率是
一枚质地均匀的正方体骰子六个面上标有数字1、2、3、4、5、6.随机抛掷这枚骰子一次,把着地一面的数字记做P点的横坐标,将该数的3倍记做P点的纵坐标.如图,抛物线y=-x2+4x+5与x轴负半轴交于点A,点B(4,5)在该抛物线上,则点P落在抛物线与直线AB围成的区域内(阴影部分,含边界)的概率是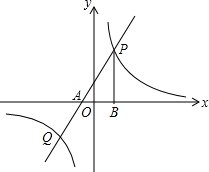 如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=
如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=