题目内容
4. 如图,二次函数y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3的图象与x轴交于A、B两点,与C轴交于点C.
如图,二次函数y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3的图象与x轴交于A、B两点,与C轴交于点C.(1)求点A、B、C的坐标;
(2)在线段AB上是否存在点P,使得∠PCB=∠BAC?如果存在,求出P点的坐标;如果不存在,说明理由;
(3)设点G、H是二次函数图象在x轴上方的两个动点,试猜想:是否存在这样的点G、H,使△AGH≌△ABH?如果存在,请举例验证你的猜想?如果不存在,请说明理由.
分析 (1)根据抛物线的性质和坐标轴上点的特点,求出点A,B,C的坐标;
(2)先判断出△PBC∽△CBA,得到$\frac{BP}{BC}=\frac{BC}{BA}$,建立方程从而求得a即可;
(3)先判断出符合要求的点G,即点G和点C重合,然后说明△AGH≌△ABH即可.
解答 解:(1)令y=0,得,-$\frac{3}{4}$x2-$\frac{9}{4}$x+3=0,
∴x1=1,x2=-4,
∴A(-4,0),B(1,0),
令x=0,得,y=3,
∴C(0,3)
(2)假设存在点P(a,0),使得∠PCB=∠BAC,
∵∠PCB=∠BAC,∠PBC=∠CBA,
∴△PBC∽△CBA,
∴$\frac{BP}{BC}=\frac{BC}{BA}$,
∵BC=$\sqrt{10}$,BA=5,
∴$\frac{1-a}{\sqrt{10}}=\frac{\sqrt{10}}{5}$,
∴a=-1,
∴存在点P(-1,0);
(3)存在点G,H,使△AGH≌△ABH,
如图,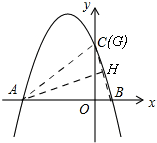
∵A(-4,0),C(0,3),B(1,0)
∴AB=5,AC=5,
∴AB=AC,
故点C就是符合要求的一个点G,
作∠BAC的平分线交抛物线于点H,连接BH,CH(GH),
∴∠CAH=∠BAH,
∵AH=AH,
∴△AGH≌△ABH,
∴当点G和点C重合时,△AGH≌△ABH.
点评 此题是二次函数综合题,主要考查了抛物线的性质,坐标轴上点的特点,相似三角形的性质和判定,全等三角形的性质和判定,解本题的关键是判断三角形相似和全等.

练习册系列答案
相关题目
19. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
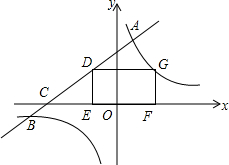 如图,直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=$\frac{3}{2}$,CE=2,点A的横坐标是1.
如图,直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=$\frac{3}{2}$,CE=2,点A的横坐标是1. 已知数轴上数a、b、c对应点的位置如图所示,化简|c-b|+|c-a|-|b-a|.
已知数轴上数a、b、c对应点的位置如图所示,化简|c-b|+|c-a|-|b-a|.