题目内容
18．不等式组$\left\{\begin{array}{l}{2x-1≤1}\\{-\frac{1}{2}x＜1}\end{array}\right.$的整数解的个数为（ ）| A． | 0个 | B． | 2个 | C． | 3个 | D． | 无数个 |
分析 先根据一元一次不等式组的解法求出x的取值范围，然后找出整数解的个数．
解答 解：解不等式2x-1≤1得：x≤1，
解不等式-$\frac{1}{2}$x＜1得：x＞-2，
则不等式组的解集为：-2＜x≤1，
整数解为：-1，0，1，共3个．
故选C．
点评 此题考查了是一元一次不等式组的整数解，解答本题的关键是根据x的取值范围，得出x的整数解．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
相关题目
8．
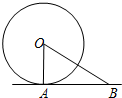如图，直线AB与⊙O相切于点A，⊙O的半径为2，若∠OBA=30°，则AB的长为（ ）
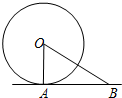如图，直线AB与⊙O相切于点A，⊙O的半径为2，若∠OBA=30°，则AB的长为（ ）| A． | 4$\sqrt{3}$ | B． | 4 | C． | 2$\sqrt{3}$ | D． | 2 |
9．
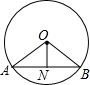如图所示，⊙O的半径为13，弦AB的长度是24，ON⊥AB，垂足为N，则ON=（ ）
如图所示，⊙O的半径为13，弦AB的长度是24，ON⊥AB，垂足为N，则ON=（ ）| A． | 5 | B． | 7 | C． | 9 | D． | 11 |
13．下列说法正确的是（ ）
| A． | 了解飞行员视力的达标率应使用抽样调查 | |
| B． | 一组数据3，6，6，7，9的中位数是6 | |
| C． | 从2000名学生中选200名学生进行抽样调查，样本容量为2000 | |
| D． | 一组数据1，2，3，4，5的方差是10 |
3．
如图，AB∥EF，CD⊥EF于点D，若∠ABC=40°，则∠BCD=（ ）
如图，AB∥EF，CD⊥EF于点D，若∠ABC=40°，则∠BCD=（ ）| A． | 140° | B． | 130° | C． | 120° | D． | 110° |
10．下列各数：1.414，$\sqrt{2}$，-$\frac{1}{3}$，0，其中是无理数的为（ ）
| A． | 1.414 | B． | $\sqrt{2}$ | C． | -$\frac{1}{3}$ | D． | 0 |
如图，抛物线l：y=-x2+bx+c（b，c为常数），其顶点E在正方形ABCD内或边上，已知点A（1，2），B（1，1），C（2，1）．