题目内容
8．
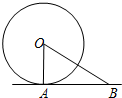如图，直线AB与⊙O相切于点A，⊙O的半径为2，若∠OBA=30°，则AB的长为（ ）| A． | 4$\sqrt{3}$ | B． | 4 | C． | 2$\sqrt{3}$ | D． | 2 |
分析 由切线的性质得∠OAB=90°，利用锐角三角函数的定义可得AB．
解答 解：∵$AB\\;为切线$，为切线，
∴∠OAB=90°，
∵∠OBA=30°，OA=2，
∴AB=$\frac{OA}{tan30°}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$，
故选C．
点评 本题主要考查了切线的性质，利用切线的性质和锐角三角函数的定义是解答此题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
16．
如图，在Rt△ABC中，∠A=30°，BC=2$\sqrt{3}$，以直角边AC为直径作⊙O交AB于点D，则图中阴影部分的面积是（ ）
如图，在Rt△ABC中，∠A=30°，BC=2$\sqrt{3}$，以直角边AC为直径作⊙O交AB于点D，则图中阴影部分的面积是（ ）| A． | $\frac{15\sqrt{3}}{4}$-$\frac{3}{2}π$ | B． | $\frac{15\sqrt{3}}{2}$-$\frac{3}{2}π$ | C． | $\frac{7\sqrt{3}}{4}$-$\frac{π}{6}$ | D． | $\frac{7\sqrt{3}}{2}$-$\frac{π}{6}$ |
如图，⊙O是△ABC的外接圆，BC是⊙O的直径，∠ABC=30°，过点B作⊙O的切线BD，与CA的延长线交于点D，与半径AO的延长线交于点E，过点A作⊙O的切线AF，与直径BC的延长线交于点F．
13．关于?ABCD的叙述，正确的是（ ）
| A． | 若AB⊥BC，则?ABCD是菱形 | B． | 若AC⊥BD，则?ABCD是正方形 | ||
| C． | 若AC=BD，则?ABCD是矩形 | D． | 若AB=AD，则?ABCD是正方形 |
20．一组数据1，8，5，3，3的中位数是（ ）
| A． | 3 | B． | 3.5 | C． | 4 | D． | 5 |