题目内容
 如图,l1∥l2∥l3,DE=6,EF=9,AB=4,则AC=
如图,l1∥l2∥l3,DE=6,EF=9,AB=4,则AC=考点:平行线分线段成比例
专题:
分析:根据平行线分线段成比例定理得出比例式,代入求出BC即可.
解答:解:∵l1∥l2∥l3,
∴
=
,
∵DE=6,EF=9,AB=4,
∴
=
,
∴BC=6,
∴AC=6+6=12.
故答案为:12.
∴
| DE |
| EF |
| AB |
| BC |
∵DE=6,EF=9,AB=4,
∴
| 6 |
| 9 |
| 4 |
| BC |
∴BC=6,
∴AC=6+6=12.
故答案为:12.
点评:本题考查了平行线分线段成比例定理的应用,解此题的关键是能够根据平行线分线段成比例定理得出比例式,难度适中.

练习册系列答案
相关题目
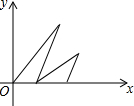 如图,若将图中的五个点的纵坐标保持不变,横坐标分别变成原来的4倍,连接各点所得图案与原图案相比( )
如图,若将图中的五个点的纵坐标保持不变,横坐标分别变成原来的4倍,连接各点所得图案与原图案相比( )| A、相同 | ||
B、横向缩短为原来的
| ||
| C、横向拉长为原来的2倍 | ||
| D、横向拉长为原来的4倍 |
下列各式中正确的是( )
| A、-(-a3)4=a12 |
| B、(-an)2=(-a2)n |
| C、(-a-b)3=(a-b)3 |
| D、(a-b)4=(-a+b)4 |
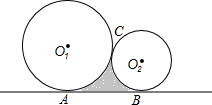 如图,一台机器的大轮⊙O1和小轮⊙O2外切于点C,且两轮分别和板面相切于A,B两点.若⊙O1的半径为3cm,⊙O2的半径为1cm,求阴影部分面积.
如图,一台机器的大轮⊙O1和小轮⊙O2外切于点C,且两轮分别和板面相切于A,B两点.若⊙O1的半径为3cm,⊙O2的半径为1cm,求阴影部分面积.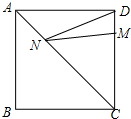 如图,正方形ABCD的边长为12,M是CD上一点,且DM=7,N是AC上一动点,则DN+MN的最小值是
如图,正方形ABCD的边长为12,M是CD上一点,且DM=7,N是AC上一动点,则DN+MN的最小值是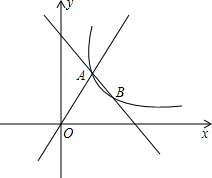 如图,直线y=3x与双曲线y=
如图,直线y=3x与双曲线y= 已知∠AOB=
已知∠AOB=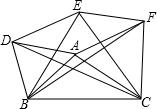 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE、EF判断哪几个三角形与△ABC全等,并证明四边形ADEF是平行四边形.
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE、EF判断哪几个三角形与△ABC全等,并证明四边形ADEF是平行四边形.