题目内容
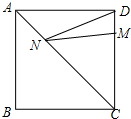如图，正方形ABCD的边长为12，M是CD上一点，且DM=7，N是AC上一动点，则DN+MN的最小值是考点：轴对称-最短路线问题
专题：
分析：要使DN+MN最小，首先应分析点N的位置．根据正方形的性质：正方形的对角线互相垂直平分，知点D的对称点是点B，连接MB交AC于点N，此时DN+MN最小值即是BM的长．
解答：
解：根据题意，连接BD、BM，则BM就是所求DN+MN的最小值，
在Rt△BCM中，BC=12，CM=CD-DM=12-7=5
根据勾股定理得：BM=
=
=13，
即DN+MN的最小值是13．
故答案为13．
解：根据题意，连接BD、BM，则BM就是所求DN+MN的最小值，在Rt△BCM中，BC=12，CM=CD-DM=12-7=5
根据勾股定理得：BM=
| BC2+CM2 |
| 122+52 |
即DN+MN的最小值是13．
故答案为13．
点评：此题考查了轴对称-最短路线问题，难点在于确定满足条件的点N的位置：利用轴对称的方法．然后熟练运用勾股定理．
练习册系列答案
天天向上口算本系列答案
相关题目
下列说法正确的是（ ）
| A、近似数4.60精确到十分位 |
| B、近似数5000万精确到个位 |
| C、近似数4.31万精确到0.01 |
| D、1.45×104精确到百位 |
如图所示，AD、CE是△ABC的高，AB=10，BD=8，CD=4，AD=6，求CE的长．
如图，点D、E分别AB、AC上，且∠ABC=∠AED．若DE=4，AE=5，BC=8，则AB的长为（ ）| A、4 | B、6 | C、8 | D、10 |
如图，l1∥l2∥l3，DE=6，EF=9，AB=4，则AC=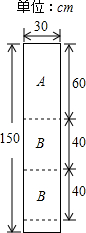
某公司装修需用A型板材240块，B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm．现只能购得规格是150cm×30cm的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（如图是裁法一的裁剪示意图）
如果y轴上有两点P（0，y1）、Q（0，y2）（y1＜y2），那么线段PQ的长为多少？
如图，在△ABC中，DE是边BC的中垂线，DE分别与边AB、BC相交于点D、E．