题目内容
18.已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-2,x2=4,则m+n的值是( )| A. | -10 | B. | 10 | C. | -6 | D. | 2 |
分析 根据根与系数的关系得出-2+4=-m,-2×4=n,求出即可.
解答 解:∵关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-2,x2=4,
∴-2+4=-m,-2×4=n,
解得:m=-2,n=-8,
∴m+n=-10,
故选A.
点评 本题考查了根与系数的关系的应用,能根据根与系数的关系得出-2+4=-m,-2×4=n是解此题的关键.

练习册系列答案
相关题目
9.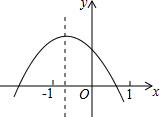 已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
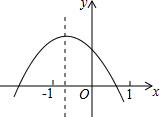 已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )| A. | a+b+c>0 | B. | b2-4ac<0 | C. | a-b+c>0 | D. | ab<0,c<0 |
7. 如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
 如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )| A. | CE=DE | B. | AE=OE | C. | $\widehat{BC}$=$\widehat{BD}$ | D. | △OCE≌△ODE |
8.下列四个数中,为无理数的是( )
| A. | $\sqrt{\frac{1}{16}}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | $\root{3}{9}$ |
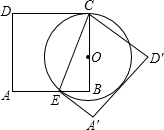 如图,矩形ABCD中,AD=4,O是BC边上的点,以OC为半径作⊙O交AB于点E,BE=$\frac{3}{5}$AE,把四边形AECD沿着CE所在的直线对折(线段AD对应A′D′),当⊙O与A′D′相切时,线段AB的长是$\frac{32}{9}$.
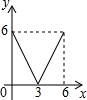
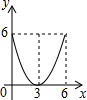
如图,矩形ABCD中,AD=4,O是BC边上的点,以OC为半径作⊙O交AB于点E,BE=$\frac{3}{5}$AE,把四边形AECD沿着CE所在的直线对折(线段AD对应A′D′),当⊙O与A′D′相切时,线段AB的长是$\frac{32}{9}$.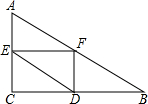 已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )
已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )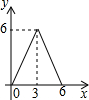
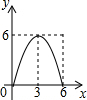
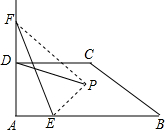 如图,四边形纸片ABCD中,AB∥CD,AD⊥AB,AB=10,AD=2$\sqrt{3}$,CD=4,点E是线段AB上的一动点,点F是射线AD上的一动点.将△AEF沿EF翻折,点A的落点记为P,连接PD.
如图,四边形纸片ABCD中,AB∥CD,AD⊥AB,AB=10,AD=2$\sqrt{3}$,CD=4,点E是线段AB上的一动点,点F是射线AD上的一动点.将△AEF沿EF翻折,点A的落点记为P,连接PD.