题目内容
18.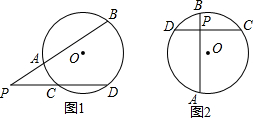 (1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.
(1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.(2)当点P在圆内时,猜想$\widehat{AC}$的度数、$\widehat{BD}$的度数与∠APC之间的数量关系,并进行证明.
分析 (1)连接AC,BD,根据圆内接四边形和圆周角定理进行计算即可得到答案;
(2)连接BD、BC、CA,根据三角形的外角的性质和圆周角定理计算即可.
解答 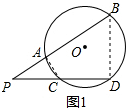 解:(1)连接AC,BD,
解:(1)连接AC,BD,
∵四边形ABDC是圆内接四边形,
∴∠ACP=∠B,∠CAP=∠D,
∵∠P=∠BAC-∠PAC
=∠BAC-∠B
=$\frac{1}{2}$($\widehat{BD}$+$\widehat{CD}$)的度数-$\frac{1}{2}$($\widehat{AC}$+$\widehat{CD}$)的度数
=$\frac{1}{2}$($\widehat{BD}$-$\widehat{AC}$+)的度数;
(2)连接BD、BC、CA,
∵∠APC=∠PBC+∠PCB
=$\frac{1}{2}$$\widehat{AC}$的度数+$\frac{1}{2}$$\widehat{BD}$ 的度数.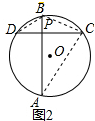
点评 本题考查的是圆周角定理、三角形的外角的性质和圆内接四边形的性质,掌握圆周角定理和三角形的外角的性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.使代数式$\frac{\sqrt{x}}{3x-1}$有意义的x的取值范围是( )
| A. | x≥0 | B. | x≠$\frac{1}{3}$ | C. | x取一切实数 | D. | x≥0且x≠$\frac{1}{3}$ |
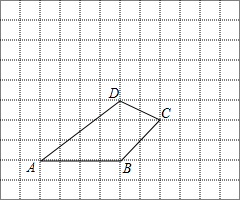 如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.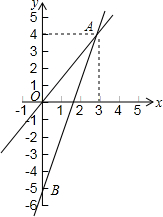 如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.
如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.



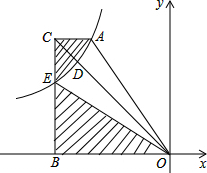 如图,在平面直角坐标系中,四边形AOBC中,∠ACB=∠CBO=90°,过A点的双曲线y=$\frac{k}{x}$的一支在第二象限交OC于点D,交边BC于点E,且$\frac{OD}{CD}$=2,S△ACD=5,则S△OBE=12.
如图,在平面直角坐标系中,四边形AOBC中,∠ACB=∠CBO=90°,过A点的双曲线y=$\frac{k}{x}$的一支在第二象限交OC于点D,交边BC于点E,且$\frac{OD}{CD}$=2,S△ACD=5,则S△OBE=12.