题目内容
8.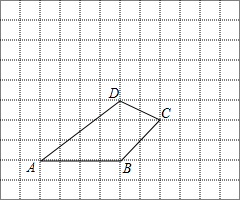 如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系.写出点A、B、C、D的坐标;
(2)求出四边形ABCD的面积.
分析 (1)先画出直角坐标系,然后利用点的坐标的表示方法分别写出点A、B、C、D的坐标;
(2)根据三角形面积公式,利用四边形ABCD的面积=S△ABD+S△BCD进行计算.
解答 解:(1)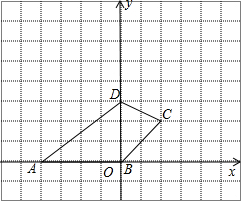 如图,
如图,
A(-4,0),B(0,0),C(2,2),D(0,3);
(2)四边形ABCD的面积=S△ABD+S△BCD
=$\frac{1}{2}$×4×3+$\frac{1}{2}$×3×2
=9.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了三角形面积公式.

练习册系列答案
相关题目
2.两数和为负数,那么这两数必定是( )
| A. | 同为正数 | B. | 同为负数 | ||
| C. | 一个为零一个为负数 | D. | 至少一个为负数,且负数绝对值大 |
13.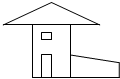 如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
 如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
如图所示的是一座房子的平面图,组成这幅图的几何图形有( )| A. | 三角形、长方形 | B. | 三角形、正方形、长方形 | ||
| C. | 三角形、正方形、长方形、梯形 | D. | 正方形、长方形、梯形 |
17.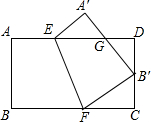 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )| A. | 9:4 | B. | 3:2 | C. | 16:9 | D. | 4:3 |
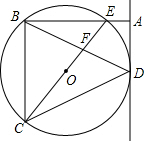 如图,⊙O为△BCD的外接圆,CE为⊙O的直径,过D作⊙O的切线交BE的延长线于A,且AD∥BC,BD交CE于F.
如图,⊙O为△BCD的外接圆,CE为⊙O的直径,过D作⊙O的切线交BE的延长线于A,且AD∥BC,BD交CE于F.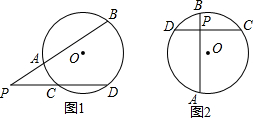 (1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.
(1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.