题目内容
10.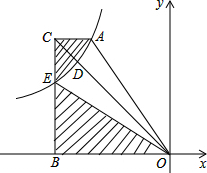 如图,在平面直角坐标系中,四边形AOBC中,∠ACB=∠CBO=90°,过A点的双曲线y=$\frac{k}{x}$的一支在第二象限交OC于点D,交边BC于点E,且$\frac{OD}{CD}$=2,S△ACD=5,则S△OBE=12.
如图,在平面直角坐标系中,四边形AOBC中,∠ACB=∠CBO=90°,过A点的双曲线y=$\frac{k}{x}$的一支在第二象限交OC于点D,交边BC于点E,且$\frac{OD}{CD}$=2,S△ACD=5,则S△OBE=12.
分析 设D(m,$\frac{k}{m}$),根据$\frac{OD}{CD}$=2表示出B、C的横坐标为$\frac{3}{2}$m,再代入解析式求出A的横坐标,利用△AOC的面积公式求出k的值,从而计算出结果.
解答 解:设D(m,$\frac{k}{m}$),
∵$\frac{OD}{CD}$=2,
∴B、C的横坐标为$\frac{3}{2}$m,
A、C的纵坐标为$\frac{3}{2}$•$\frac{k}{m}$=$\frac{3k}{2m}$,
∴A的横坐标x=k÷$\frac{3k}{2m}$=$\frac{2m}{3}$,
∴AC=$\frac{2m}{3}$-$\frac{3m}{2}$=-$\frac{5m}{6}$,
∴S△AOC=$\frac{1}{2}$AC•AB
=$\frac{1}{2}$(-$\frac{5m}{6}$)•$\frac{3k}{2m}$
=-$\frac{5}{8k}$=15,
∴k=-24,
∴S△OBE=$\frac{1}{2}$|k|=12,
故答案为:12.
点评 本题考查了反比例函数系数k的几何意义,利用解析式即比值求出k的值,从而求出三角形的面积是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列各曲线表示的y与x的关系中,y不是x的函数的是( )
| A. | 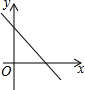 | B. | 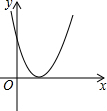 | ||
| C. | 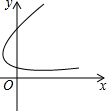 | D. | 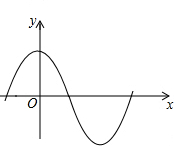 |
20.已知样本数据为1,2,3,4,5,则它的方差为( )
| A. | 10 | B. | $\sqrt{10}$ | C. | 2 | D. | $\sqrt{2}$ |
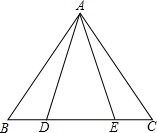 如图,△ABC中,点D、E在BC边上,∠BAD=∠CAE请你添加一对相等的线段或一对相等的角的条件,使△ABD≌△ACE.你所添加的条件是AB=AC.
如图,△ABC中,点D、E在BC边上,∠BAD=∠CAE请你添加一对相等的线段或一对相等的角的条件,使△ABD≌△ACE.你所添加的条件是AB=AC.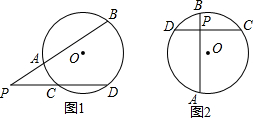 (1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.
(1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.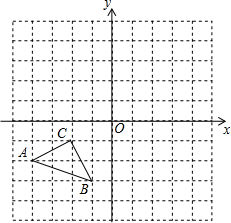 已知△ABC各顶点的坐标为A(-4,-2),B(-1,-3),C(-2,-1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度得到△A′B′C′.
已知△ABC各顶点的坐标为A(-4,-2),B(-1,-3),C(-2,-1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度得到△A′B′C′.