题目内容
13.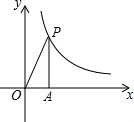 如图,已知点P(x,y)是反比例函数图象上一点,O是坐标原点,PA⊥x轴,S△PAO=4,且图象经过(1,3m-1);求:
如图,已知点P(x,y)是反比例函数图象上一点,O是坐标原点,PA⊥x轴,S△PAO=4,且图象经过(1,3m-1);求:(1)反比例函数解析式.
(2)m的值.
分析 (1)此题可从反比例函数系数k的几何意义入手,△PAO的面积为点P向两条坐标轴作垂线,与坐标轴围成的矩形面积的一半即S=$\frac{1}{2}$|k|,再结合反比例函数所在的象限确定出k的值,则反比例函数的解析式即可求出;
(2)将(1,3m-1)代入解析式即可得出m的值.
解答 解:(1)设反比例函数解析式为$y=\frac{k}{x}$,
∵过点P(x,y),
∴$\frac{1}{2}$xy=4,
∴xy=8,
∴k=xy=8,
∴反比例函数解析式是:$y=\frac{8}{x}$;
(2)∵图象经过(1,3m-1),
∴1×(3m-1)=8,
∴m=3.
点评 本题主要考查了反比例函数$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形面积为$\frac{1}{2}$|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
3.计算(0.04)2013×[(-5)2012]2的正确结果是( )
| A. | 0.04 | B. | -5 | C. | 3 | D. | 4 |
8.下列命题中,正确的是( )
| A. | 有两边和一角对应相等的两个三角形全等 | |
| B. | 有三个角对应相等的两个三角形全等 | |
| C. | 有一边和两角对应相等的两个三角形全等 | |
| D. | 以上答案都不对 |
2.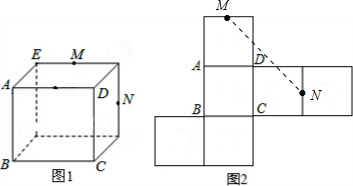 图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
 图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )| A. | 11$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | 10 | D. | 8 |

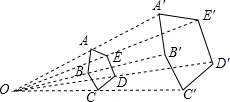 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形,A′B′C′D′E′,已知OA=10cm,OA′=20cm,五边形ABCDE的周长为15cm,则五边形A′B′C′D′E′的周长为30cm.
如图,以点O为位似中心,将五边形ABCDE放大后得到五边形,A′B′C′D′E′,已知OA=10cm,OA′=20cm,五边形ABCDE的周长为15cm,则五边形A′B′C′D′E′的周长为30cm.