题目内容
15. 如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.
如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.(1)求证:BE=AF;
(2)连接DF,试探究当△ABC满足什么条件时,使得四边形BEDF是菱形,并说明理由.
分析 (1)先证明四边形ADEF是平行四边形,再根据平行四边形的性质和等量关系即可证明结论成立;
(2)根据一组邻边相等的平行四边形是菱形可以解答本题.
解答 (1)证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBC,
∵DE∥AB,
∴∠ABD=∠DBE,
∴∠BDE=∠DBE,
∴BE=DE,
∵EF∥AC,
∴四边形ADEF是平行四边形,
∴AF=DE,
∴AF=BE;
(2)解:当AB=BC时,四边形BEDF是菱形,理由如下:
∵AB=BC,
∴∠A=∠C,
∵EF∥AC,
∴∠A=∠BFE,∠C=∠BFE,
∴∠BFE=∠BFE,
∴BF=BE,
∵DE=BE,
∴BF=DE,
∵DE∥AB,
∴四边形BEDF是菱形.
点评 本题考查平行四边形的判定与性质、菱形的判定,解答本题的关键是明确题意,找出所求问题需要的需要的条件,利用平行四边形的判定与性质、菱形的判定解答.

练习册系列答案
相关题目
6.通过调查,一段时间内,C、D两城生产化肥供给A、B两乡,其中A、B两乡需求总量y(吨)与化肥市场价格x(百元/吨)(3≤x≤8),存在下列关系:
C、D两城生产总量Z(吨)与化肥市价x(百元/吨)成正比例函数:Z=100x,已知C城生产总量为240吨,A乡需求量为200吨.如果需求量y与生产量Z相等,此时处于平衡状态.
(1)请通过描点画图,探究y与x之间的函数关系;
(2)某运输公司承担化肥运输任务,已知从C城运往A、B两乡运费分别为20元/t和15元/t;从D城运往A、B两乡费用分别未能25元/t和24元/t,当市场处于平衡状态时,如何调运可使总费用最少?并求出最小费用是多少元?
| x | 4 | 5 | 6 | 7 |
| y | 550 | 500 | 450 | 400 |
(1)请通过描点画图,探究y与x之间的函数关系;
(2)某运输公司承担化肥运输任务,已知从C城运往A、B两乡运费分别为20元/t和15元/t;从D城运往A、B两乡费用分别未能25元/t和24元/t,当市场处于平衡状态时,如何调运可使总费用最少?并求出最小费用是多少元?
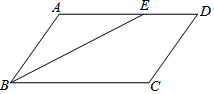 如图,在?ABCD中,ED=2,BC=5,∠ABC的平分线交AD于点E,则AB的长为3.
如图,在?ABCD中,ED=2,BC=5,∠ABC的平分线交AD于点E,则AB的长为3.
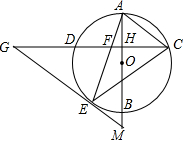 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.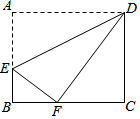 如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.
如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.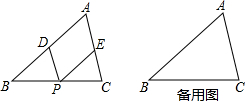 在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.
在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.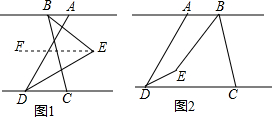
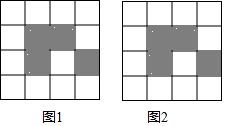 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.