题目内容
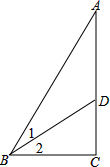如图，△ABC中，∠C=90°，∠1=∠2，BC=54cm，BD=36| 3 |
（1）∠2的度数；
（2）AC的长．（不允许使用计算器）
考点：解直角三角形
专题：
分析：（1）直接利用锐角三角函数关系得出∠2的度数；
（2）利用已知得出∠ABC的度数，进而得出AC的长．
（2）利用已知得出∠ABC的度数，进而得出AC的长．
解答：解：（1）∵△ABC中，∠C=90°，BC=54cm，BD=36
cm，
∴cos∠2=
=
=
，
∴∠2=30°；
（2）∵∠1=∠2，∠2=30°，
∴∠1=∠2=30°，
∴∠ABC=60°，
∴tan60°=
，
∴AC=BC×
=54
（cm）．
| 3 |
∴cos∠2=
| 54 | ||
36
|
| 3 | ||
2
|
| ||
| 2 |
∴∠2=30°；
（2）∵∠1=∠2，∠2=30°，
∴∠1=∠2=30°，
∴∠ABC=60°，
∴tan60°=
| AC |
| BC |
∴AC=BC×
| 3 |
| 3 |
点评：此题主要考查了解直角三角形，正确选择锐角三角函数关系是解题关键．
练习册系列答案
相关题目
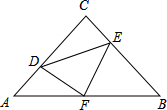如图，在等腰直角三角形ABC中，∠C=90°，AC=8，点F是AB的中点，点D、E分别在AC、BC边上运动，且始终保持DF⊥EF，则四边形CDFE的面积是在离地面高度为5米处引拉线固定电线杆，拉线与地面成60°的角，则拉线的长是（ ）
| A、10 | ||||
B、
| ||||
C、
| ||||
D、5
|
已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结论：①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，其中正确的结论是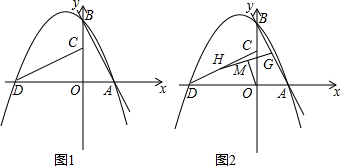
如图，在△ABC中，∠A=60°，BD、CE分别是AC与AB边上的高，求证：BC=2DE．
如图，在△ABC中，点D在边AB上，BD=2AD，DE∥BC交AC于点E，若S△ADE=1，则S△ABC为（ ）