题目内容
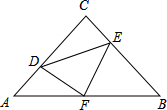 如图,在等腰直角三角形ABC中,∠C=90°,AC=8,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则四边形CDFE的面积是
如图,在等腰直角三角形ABC中,∠C=90°,AC=8,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则四边形CDFE的面积是考点:全等三角形的判定与性质
专题:
分析:连接CF,易证△ADF≌△CEF,即可求得四边形CDFE面积=S△ACF,根据AC可以求得AF,CF的值,即可解题.
解答:解:连接CF,
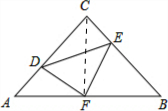
∵AC=BC,∠ACB=90°,
∴CF=AF,∠A=∠FCB=90°,
∵∠AFD+∠CFD=90°,∠CFD+∠CFE=90°,
∴∠AFD=∠CFE,
在△ADF和△CEF中,
,
∴△ADF≌△CEF(ASA),
∴四边形CDFE面积=S△ACF,
∵AC=8,CF=AF,
∴CF=
=4
,
∴四边形CDFE面积=S△ACF=
×4
×4
=16,
故答案为:16.

∵AC=BC,∠ACB=90°,
∴CF=AF,∠A=∠FCB=90°,
∵∠AFD+∠CFD=90°,∠CFD+∠CFE=90°,
∴∠AFD=∠CFE,
在△ADF和△CEF中,
|
∴△ADF≌△CEF(ASA),
∴四边形CDFE面积=S△ACF,
∵AC=8,CF=AF,
∴CF=
| 8 | ||
|
| 2 |
∴四边形CDFE面积=S△ACF=
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:16.
点评:本题考查了全等三角形的判定,考查了全等三角形面积相等的性质,本题中求证△ADF≌△CEF是解题的关键.

练习册系列答案
相关题目
“井底之蛙”要爬出来,他每小时爬上5米,休息一小时又滑下3米,若井深11米,则它爬出井来需要( )小时.
| A、5 | B、6 | C、7 | D、8 |
一个几何体由若干大小相同的小正方形搭成,从正面、上面看到的这个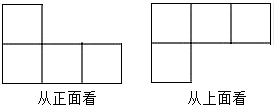 几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
 几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )| A、4个 | B、5个 | C、6个 | D、7个 |
 如图,在△ABC中,∠ACB=90°,AD⊥AB,AD=AB,BE⊥DC,AF⊥AC,求证:CF平分∠ACB.
如图,在△ABC中,∠ACB=90°,AD⊥AB,AD=AB,BE⊥DC,AF⊥AC,求证:CF平分∠ACB. 如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.
如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个. 某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.
某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.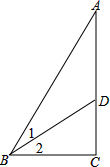 如图,△ABC中,∠C=90°,∠1=∠2,BC=54cm,BD=36
如图,△ABC中,∠C=90°,∠1=∠2,BC=54cm,BD=36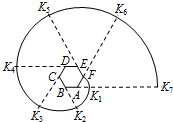 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )