题目内容
 如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,若S△ADE=1,则S△ABC为( )
如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,若S△ADE=1,则S△ABC为( )| A、3 | B、4 | C、8 | D、9 |
考点:相似三角形的判定与性质
专题:
分析:由平行可得△ADE∽△ABC,则BD=2AD,可求得AD:AB=1:3,再利用面积比等于相似比的平方,可求得△ABC的面积.
解答:解:
∵BD=2AD,
∴
=
=
,
∵DE∥BC,
∴△ADE∽△ABC,
∴
=(
)2=(
)2=
,
即
=
,
解得S△ABC=9,
故选D.
∵BD=2AD,
∴
| AD |
| AB |
| AD |
| 3AD |
| 1 |
| 3 |
∵DE∥BC,
∴△ADE∽△ABC,
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
| 1 |
| 3 |
| 1 |
| 9 |
即
| 1 |
| S△ABC |
| 1 |
| 9 |
解得S△ABC=9,
故选D.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
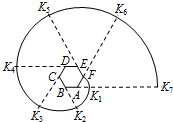 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
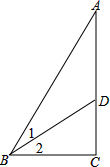 如图,△ABC中,∠C=90°,∠1=∠2,BC=54cm,BD=36
如图,△ABC中,∠C=90°,∠1=∠2,BC=54cm,BD=36