题目内容
 如图,在△ABC中,∠A=60°,BD、CE分别是AC与AB边上的高,求证:BC=2DE.
如图,在△ABC中,∠A=60°,BD、CE分别是AC与AB边上的高,求证:BC=2DE.考点:相似三角形的判定与性质
专题:证明题
分析:证明B、C、D、E四点共圆,进而证明△AED∽△ACB,得到
=
;证明AB=2AD问题即可解决.
| DE |
| BC |
| AD |
| AB |
解答: 证明:∵BD、CE分别是AC与AB边上的高,
证明:∵BD、CE分别是AC与AB边上的高,
∴∠BEC=∠BDC,
∴B、C、D、E四点共圆,
∴∠AED=∠ACB,而∠A=∠A,
∴△AED∽△ACB,
∴
=
;
∵BD⊥AC,且∠A=60°,
∴∠ABD=30°,AD=
AB,
∴BC=2DE.
 证明:∵BD、CE分别是AC与AB边上的高,
证明:∵BD、CE分别是AC与AB边上的高,∴∠BEC=∠BDC,
∴B、C、D、E四点共圆,
∴∠AED=∠ACB,而∠A=∠A,
∴△AED∽△ACB,
∴
| DE |
| BC |
| AD |
| AB |
∵BD⊥AC,且∠A=60°,
∴∠ABD=30°,AD=
| 1 |
| 2 |
∴BC=2DE.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
一个几何体由若干大小相同的小正方形搭成,从正面、上面看到的这个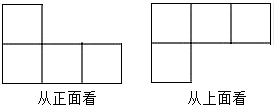 几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
 几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )| A、4个 | B、5个 | C、6个 | D、7个 |
若关于x的函数y=kx2+2x-1与x轴只有一个交点,则实数k的值为( )
| A、-1 | B、-2 | C、1 | D、2 |
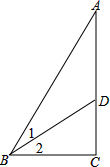 如图,△ABC中,∠C=90°,∠1=∠2,BC=54cm,BD=36
如图,△ABC中,∠C=90°,∠1=∠2,BC=54cm,BD=36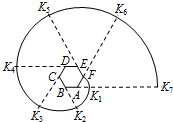 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )