题目内容
 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结论:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0,其中正确的结论是
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结论:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0,其中正确的结论是考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线与x轴有2个交点得到b2-4ac>0,即b2>4ac;由抛物线开口方向得到a>0,由抛物线的对称轴为直线x=-
=1得到b=2a>0,由抛物线与y轴的交点在x轴下方得到c<0,所以abc<0;由x=1时,函数值为正数得到a+b+c>0;由x=-1时,函数值为负数得到a-b+c<0.
| b |
| 2a |
解答:解:∵抛物线与x轴有2个交点,
∴b2-4ac>0,
即b2>4ac,所以①正确;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-
=-1,
∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以②错误;
∵b=2a,
∴2a-b=0,所以③错误;
∵x=1时,y>0,
∴a+b+c>0,所以④正确;
∵x=-1时,y<0,
∴a-b+c<0,所以⑤正确.
故答案为①④⑤.
∴b2-4ac>0,
即b2>4ac,所以①正确;
∵抛物线开口向上,

∴a>0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以②错误;
∵b=2a,
∴2a-b=0,所以③错误;
∵x=1时,y>0,
∴a+b+c>0,所以④正确;
∵x=-1时,y<0,
∴a-b+c<0,所以⑤正确.
故答案为①④⑤.
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0.

练习册系列答案
相关题目
使用墙的一边,再用13m的铁丝网围成三边,围成一个面积为20m2的长方形,求这个长方形的两边长.设墙的对边长为xm,可得方程( )
| A、x(13-x)=20 | ||
B、x•
| ||
C、x(13-
| ||
D、x•
|
 如图,在△ABC中,∠ACB=90°,AD⊥AB,AD=AB,BE⊥DC,AF⊥AC,求证:CF平分∠ACB.
如图,在△ABC中,∠ACB=90°,AD⊥AB,AD=AB,BE⊥DC,AF⊥AC,求证:CF平分∠ACB. 某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.
某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.
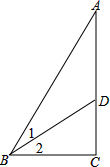 如图,△ABC中,∠C=90°,∠1=∠2,BC=54cm,BD=36
如图,△ABC中,∠C=90°,∠1=∠2,BC=54cm,BD=36