题目内容
6.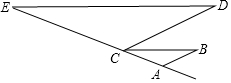 已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA
已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA证明:∵AB∥CD(已知)
∴∠B=∠BCD(两直线平行,内错角相等)
∵∠B=∠D(已知)
∴∠D=∠BCD(等量代换)
∴ED∥CB(内错角相等,两直线平行)
∴∠E=∠BCA(两直线平行,同位角相等)
分析 根据平行线的性质求出∠B=∠BCD,求出∠D=∠BCD,根据平行线的判定得出DE∥BC,根据平行线的性质得出即可.
解答 证明:∵AB∥CD(已知)
∴∠B=∠BCD(两直线平行,内错角相等)
∵∠B=∠D(已知)
∴∠D=∠BCD(等量代换)
∴ED∥CB(内错角相等,两直线平行)
∴∠E=∠BCA(两直线平行,同位角相等),
故答案为:BCD,D,BCD,内错角相等,两直线平行,两直线平行,同位角相等.
点评 本题考查了平行线的性质和判定,能灵活运用平行线的性质和判定进行推理是解此题的关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | $\sqrt{2}$-2$\sqrt{2}$=-$\sqrt{2}$ | B. | $\sqrt{8{a}^{2}}$=4a(a>0) | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |
17.化简($\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{2-x}{x+2}$)÷$\frac{x}{x-2}$,其结果是( )
| A. | -$\frac{8}{x-2}$ | B. | $\frac{8}{x-2}$ | C. | $\frac{8}{x+2}$ | D. | -$\frac{8}{x+2}$ |
18.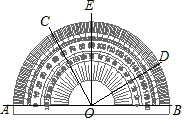 如图所示,用量角器度量几个角的度数.下列结论中正确的是( )
如图所示,用量角器度量几个角的度数.下列结论中正确的是( )
 如图所示,用量角器度量几个角的度数.下列结论中正确的是( )
如图所示,用量角器度量几个角的度数.下列结论中正确的是( )| A. | ∠BOC=60° | B. | ∠COA是∠EOD的余角 | ||
| C. | ∠AOC=∠BOD | D. | ∠AOD与∠COE互补 |
13.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
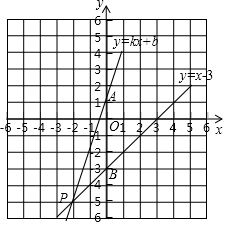 如图,已知一次函数y=kx+b经过点A(0,1)且和直线y=x-3交于点P(a,-5).
如图,已知一次函数y=kx+b经过点A(0,1)且和直线y=x-3交于点P(a,-5).