题目内容
17.给出下列四个说法:①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2;
④若三个整数a,b,c是直角三角形的三边长,则2a,2b,2c一定是勾股数,其中正确的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
分析 欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
解答 解:①由于0.32+0.42=0.52,所以以0.3,0.4,0.5为边长的三角形是直角三角形,但是0.3,0.4,0.5不是整数,所以0.3,0.4,0.5不是勾股数,故①说法错误;
②虽然以0.5,1.2,1.3为边长的三角形是直角三角形,但是0.5,1.2,1.3不是整数,所以0.5,1.2,1.3不是勾股数,故②说法错误;
③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2,故③说法正确;
④若三个整数a,b,c是直角三角形的三边长,则2a,2b,2c一定是勾股数,故④说法正确.
故选C.
点评 此题考查了勾股数:满足a2+b2=c2的三个正整数,称为勾股数.注意:
①三个数必须是正整数,例如:2.5、6、6.5满足a2+b2=c2,但是它们不是正整数,所以它们不是勾股数.
②一组勾股数扩大相同的整数倍得到的三个数仍是一组勾股数.
③记住常用的勾股数再做题可以提高速度.如:3,4,5;6,8,10;5,12,13;….

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.计算:a3•a2的结果( )
| A. | a6 | B. | 5a | C. | 6a | D. | a5 |
5.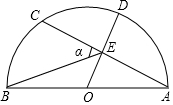 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE,设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE,设∠BEC=α,则tanα的值为( )
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE,设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE,设∠BEC=α,则tanα的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{2}{3}$ |
12. 如图,MQ为∠NMP的平分线,MP⊥NP,QT⊥MN,垂足分别为P,T,下列结论不正确的是( )
如图,MQ为∠NMP的平分线,MP⊥NP,QT⊥MN,垂足分别为P,T,下列结论不正确的是( )
 如图,MQ为∠NMP的平分线,MP⊥NP,QT⊥MN,垂足分别为P,T,下列结论不正确的是( )
如图,MQ为∠NMP的平分线,MP⊥NP,QT⊥MN,垂足分别为P,T,下列结论不正确的是( )| A. | S△MNQ=$\frac{1}{2}$MN•PQ | B. | ∠MQT=∠MQP | C. | MT=MP | D. | ∠NQP=∠MQT |
2. 如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )
如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )
 如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )
如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )| A. | 70° | B. | 110° | C. | 120° | D. | 130° |
9.比较-2,-$\frac{1}{2}$,0,0.02的大小,正确的是( )
| A. | -$\frac{1}{2}$<-2<0.02<0 | B. | -$\frac{1}{2}$<-2<0<0.02 | C. | -2<-$\frac{1}{2}$<0.02<0 | D. | -2<-$\frac{1}{2}$<0<0.02 |
6. 如图,在△ABC中,点D,E分别在AB,AC上,则添加下面的条件后,不能判断△AED∽△ABC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,则添加下面的条件后,不能判断△AED∽△ABC的是( )
 如图,在△ABC中,点D,E分别在AB,AC上,则添加下面的条件后,不能判断△AED∽△ABC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,则添加下面的条件后,不能判断△AED∽△ABC的是( )| A. | $\frac{AD}{AC}$=$\frac{DE}{BC}$ | B. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | C. | ∠AED=∠B | D. | ∠ADE=∠C |
7.当0<x<3时,化简$\sqrt{{{(x+1)}^2}}$-$\sqrt{{{(x-3)}^2}}$的正确结果是( )
| A. | 4 | B. | 2x-2 | C. | -4 | D. | 2-2x |
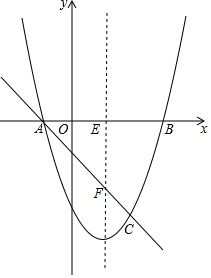 如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),点C为抛物线上一点,且点C的横坐标为2,抛物线的对称轴EF交x轴于点E,交直线AC于点F.
如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),点C为抛物线上一点,且点C的横坐标为2,抛物线的对称轴EF交x轴于点E,交直线AC于点F.