题目内容
7．当0＜x＜3时，化简$\sqrt{{{（x+1）}^2}}$-$\sqrt{{{（x-3）}^2}}$的正确结果是（ ）| A． | 4 | B． | 2x-2 | C． | -4 | D． | 2-2x |
分析 根据x的范围判断出x+1与x-3的正负，原式利用二次根式性质及绝对值的代数意义化简，去括号合并即可得到结果．
解答 解：∵0＜x＜3，
∴x+1＞0，x-3＜0，
则原式=|x+1|-|x-3|=x+1+x-3=2x-2，
故选B
点评 此题考查了二次根式的性质与化简，以及绝对值，熟练掌握运算法则及绝对值的代数意义是解本题的关键．
练习册系列答案
相关题目
18．下列命题中，真命题是（ ）
| A． | 所有的平行四边形都相似 | B． | 所有的矩形都相似 | ||
| C． | 所有的菱形都相似 | D． | 所有的正方形都相似 |
2．下列各式正确的是（ ）
| A． | $\sqrt{4\frac{4}{9}}=2\frac{2}{3}$ | B． | $\frac{{\sqrt{12}}}{3}=2$ | C． | $\sqrt{3}+\sqrt{2}=\frac{1}{{\sqrt{3}-\sqrt{2}}}$ | D． | $\sqrt{{{（-3）}^2}}=-3$ |
12．计算-34的结果是（ ）
| A． | 81 | B． | -81 | C． | 12 | D． | -12 |
19．
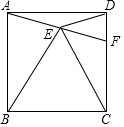如图，正方形ABCD中，以BC为边向正方形内部作等边△BCE，连接AE并延长交CD于F，连接DE，下列结论：①AE=DE；②∠CEF=45°；③AE=EF；④△DEF∽△ABE，其中正确的结论共有（ ）
如图，正方形ABCD中，以BC为边向正方形内部作等边△BCE，连接AE并延长交CD于F，连接DE，下列结论：①AE=DE；②∠CEF=45°；③AE=EF；④△DEF∽△ABE，其中正确的结论共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．下列图形中不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
已知如图，CO、CB是⊙O′的弦，⊙O′与坐标系x、y轴交于B、A两点，点A的坐标为（0，1），⊙O′的弦OB的长为$\sqrt{3}$，则∠OCB的度数为（ ）