如图.MQ为∠NMP的平分线.MP⊥NP.QT⊥MN.垂足分别为P.T.下列结论不正确的是( )A．S△MNQ=$\frac{1}{2}$MN•PQB．∠MQT=∠MQPC．MT=MPD．∠NQP=∠MQT 题目和参考答案——青夏教育精英家教网—

题目内容

12．

如图，MQ为∠NMP的平分线，MP⊥NP，QT⊥MN，垂足分别为P，T，下列结论不正确的是（　　）

A．

S_△MNQ=$\frac{1}{2}$MN•PQ

B．

∠MQT=∠MQP

C．

MT=MP

D．

∠NQP=∠MQT

分析根据角平分线的性质得到QT=QP，证明Rt△MQT≌Rt△MQP，判断即可．

解答解：∵MQ为∠NMP的平分线，MP⊥NP，QT⊥MN，
∴QT=QP，
∴S_△MNQ=$\frac{1}{2}$MN•QT=S_△MNQ=$\frac{1}{2}$MN•PQ，A不符合题意；
在Rt△MQT和Rt△MQP中，
$\left\{\begin{array}{l}{QT=QP}\\{MQ=MQ}\end{array}\right.$，
∴Rt△MQT≌Rt△MQP，
∴∠MQT=∠MQP，B不符合题意；
∴MT=MP，C不符合题意；
D符合题意，
故选：D．

点评本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．

练习册系列答案

相关题目

3．对于双曲线y=-$\frac{3}{x}$，下列说法正确的是（　　）

	A．	它的两个分支分别在一、三象限		B．	y随x的增大而增大
	C．	在每一支上，y随x的增大而增大		D．	点（3，1）在它的图象上

20．

如图，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为（2，3），双曲线y=-$\frac{k}{x}$（x＞0）的图象经过的中点D，且与AB交于点E，连接DE
（1）求△BDE的面积
（2）若点F是OC边上一点，且△FBC∽△DEB，求点F坐标．

7．下列说法正确的是（　　）

	A．	一个数的相反数一定比0小
	B．	互为相反数的两个数的绝对值相等
	C．	一个数的绝对值一定是正数
	D．	若两个数的绝对值相等，则这两个数相等

17．给出下列四个说法：
①由于0.3，0.4，0.5不是勾股数，所以以0.3，0.4，0.5为边长的三角形不是直角三角形；
②由于以0.5，1.2，1.3为边长的三角形是直角三角形，所以0.5，1.2，1.3是勾股数；
③若a，b，c是勾股数，且c最大，则一定有a²+b²=c²；
④若三个整数a，b，c是直角三角形的三边长，则2a，2b，2c一定是勾股数，其中正确的是（　　）

4．

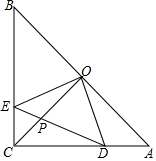如图，在等腰直角△ACB中，∠ACB=90°，O是斜边AB的中点，点D、E分别在直角边AC、BC上，且∠DOE=90°，DE交OC于点P，则下列结论
（1）△AOD≌△COE；（2）OE=OD；（3）△EOP∽△CDP．
其中正确的结论是（　　）

	A．	两条对角线相等的平行四边形是矩形
	B．	两条对角线互相垂直的四边形是菱形
	C．	两条对角线互相垂直的矩形是正方形
	D．	两条对角线互相平分的四边形是平行四边形

2．下列各式正确的是（　　）

A．

$\sqrt{4\frac{4}{9}}=2\frac{2}{3}$

B．

$\frac{{\sqrt{12}}}{3}=2$

C．

$\sqrt{3}+\sqrt{2}=\frac{1}{{\sqrt{3}-\sqrt{2}}}$

D．

$\sqrt{{{（-3）}^2}}=-3$

试题分类