题目内容
2. 如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )
如图,⊙O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为( )| A. | 70° | B. | 110° | C. | 120° | D. | 130° |
分析 先根据三角形的内角和定理求得∠B,再由切线的性质得∠BDO=∠BEO=90°,从而得出∠DOE.
解答 解:∵∠BAC=50°,∠ACB=60°,
∴∠B=180°-50°-60°=70°,
∵E,F是切点,
∴∠BDO=∠BEO=90°,
∴∠DOE=180°-∠B,
∴∠DOE=∠A+∠C=50°+60°=110°.
故选:B.
点评 此题考查了三角形的内切圆和切线长定理,是基础知识要熟练掌握,根据已知得出∠DOE=180°-∠B是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.一元二次方程x2=2x的根是( )
| A. | x1=0,x2=2 | B. | x=0 | C. | x=2 | D. | x1=0,x2=-2 |
7. 如图,在数轴上点M表示的数可能是( )
如图,在数轴上点M表示的数可能是( )
 如图,在数轴上点M表示的数可能是( )
如图,在数轴上点M表示的数可能是( )| A. | 1.5 | B. | -1.5 | C. | -2.5 | D. | 2.5 |
14.正比例函数y=(2k-3)x的图象过点(3,-9),则k的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
12.计算-34的结果是( )
| A. | 81 | B. | -81 | C. | 12 | D. | -12 |
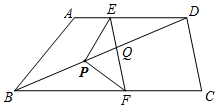 如图,在四边形ABCD中,AD∥BC,AD=6cm,BC=BD=10cm,点P由
如图,在四边形ABCD中,AD∥BC,AD=6cm,BC=BD=10cm,点P由 如图,菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,要使四边形ABCD是正方形,则需要添加一个条件是∠ABC=90°.(填一个即可)
如图,菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,要使四边形ABCD是正方形,则需要添加一个条件是∠ABC=90°.(填一个即可)