Question

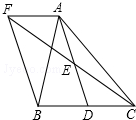如图，在△ABC中，D是BC边上一点，E是AD的中点，过A作BC的平行线交CE的延长线F，且AF=BD，连结BF．
（1）求证：BD=CD；
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论；
（3）当△ABC满足什么条件时，四边形AFBD为正方形？（写出条件即可，不要求证明）

Answer 1

考点：正方形的判定,全等三角形的判定与性质,矩形的判定

专题：

分析：（1）证明△AEF≌△DEC可得AF=DC，再根据条件AF=BD可利用等量代换可得BD=CD；
（2）首先判定四边形AFBD为平行四边形，再根据等腰三角形三线合一的性质可得AD⊥BC，进而可得四边形AFBD为矩形；
（3）当AB=AC，且∠BAC=90°时，四边形AFBD为正方形，首先证明∠ABC=45°，∠BAD=45°，可得AD=BD，进而可得四边形AFBD为正方形．

解答： （1）证明：∵AF∥BC，
∴∠AFE=∠ECD．
∵E是AD的中点，
∴DE=AE，
在△AEF与△DEC中，

∠AFE=∠ECD ∠AEF=∠DEC AE=ED

，
∴△AEF≌△DEC（AAS），
∴AF=DC，
∵AF=BD，
∴BD=CD；

（2）答：四边形AFBD为矩形；
解：∵AF=BD，AF∥BD，
∴四边形AFBD为平行四边形，
∵AB=AC，BD=DC，
∴AD⊥BC，
∴∠BDA=90°，
∴四边形AFBD为矩形；

（3）AB=AC，且∠BAC=90°；
∵AB=AC，且∠BAC=90°，
∴∠ABC=45°，
∵AD⊥BC，
∴∠BAD=45°，
∴AD=DB，
∴四边形AFBD为正方形．

点评：此题主要考查了正方形的判定，矩形的判定，以及全等三角形的判定与性质，关键是掌握邻边相等的矩形是正方形．