题目内容
已知一抛物线的顶点A的坐标是(2,9),并且抛物线与x轴两交点间的距离为6.
(1)试求该抛物线的关系式;
(2)若点B(n,5)在此抛物线上,且点B在第一象限,求以点A、B和坐标原点O为顶点的△OAB面积.
(1)试求该抛物线的关系式;
(2)若点B(n,5)在此抛物线上,且点B在第一象限,求以点A、B和坐标原点O为顶点的△OAB面积.
考点:抛物线与x轴的交点,二次函数图象上点的坐标特征,待定系数法求二次函数解析式
专题:
分析:(1)已知了抛物线的对称轴方程和抛物线与x轴两交点间的距离,可求出抛物线与x轴两交点的坐标;然后用待定系数法求出抛物线的解析式;
(2)根据(1)中的抛物线解析式得到点B的坐标,然后利用三角形的面积公式来求△OAB面积.
(2)根据(1)中的抛物线解析式得到点B的坐标,然后利用三角形的面积公式来求△OAB面积.
解答:
解:(1)∵二次函数的顶点坐标(2,9),并且图象与x轴两交点间距离为6,
∴二次函数图象与x轴两交点坐标为(-1,0)与(5,0),
设抛物线解析式为y=a(x+1)(x-5),
把(2,9)代入,得
9=a(2+1)(2-5),
解得 a=-1.
故抛物线的解析式为:y=-(x+1)(x-5)或y=-x2+4x+5.
(2)设直线x=2与直线OB交于点D.
由(1)知,抛物线的解析式为:y=-x2+4x+5.
把点B(n,5)代入,得
5=-n2+4n+5,即n(n-4)=0,
解得 n1=0,n2=4.
∵点B(n,5)在此抛物线上,且点B在第一象限,
∴B(4,5).
易求直线OB的解析式为:y=
x.
把x=2代入得到:y=
,
∴AD=9-
=
.
∴S△OAB=
AD•xB=
×
×4=13,即△OAB面积是13.
∴二次函数图象与x轴两交点坐标为(-1,0)与(5,0),
设抛物线解析式为y=a(x+1)(x-5),
把(2,9)代入,得
9=a(2+1)(2-5),
解得 a=-1.
故抛物线的解析式为:y=-(x+1)(x-5)或y=-x2+4x+5.

(2)设直线x=2与直线OB交于点D.
由(1)知,抛物线的解析式为:y=-x2+4x+5.
把点B(n,5)代入,得
5=-n2+4n+5,即n(n-4)=0,
解得 n1=0,n2=4.
∵点B(n,5)在此抛物线上,且点B在第一象限,
∴B(4,5).
易求直线OB的解析式为:y=
| 5 |
| 4 |
把x=2代入得到:y=
| 5 |
| 2 |
∴AD=9-
| 5 |
| 2 |
| 13 |
| 2 |
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
点评:本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征以及待定系数法求二次函数的解析式.求二次函数解析式时,也可以设顶点式方程来解答.

练习册系列答案
相关题目
下列方程是一元二次方程的是( )
| A、x2+2=0 | ||
| B、x2+y+6=0 | ||
C、x2+
| ||
| D、y2-2x-1=0 |
在Rt△ABC中,∠C=Rt∠,AC=3cm,AB=5cm,若以C为圆心,4cm为半径画一个圆,则下列结论中,正确的是( )
| A、点A在圆C内,点B在圆C外 |
| B、点A在圆C外,点B在圆C内 |
| C、点A在圆C上,点B在圆C外 |
| D、点A在圆C内,点B在圆C上 |
 某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据:
某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据:
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CE平分∠ACB,DE是AB的中垂线.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CE平分∠ACB,DE是AB的中垂线.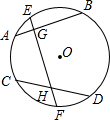 已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证:
已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证: