题目内容
13.(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=4$\sqrt{2}$.①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.

分析 (1)①连结OA、OC,如图1,利用勾股定理的逆定理证明△OCA为等腰直角三角形,∠AOC=90°,然后根据圆周角定理易得∠ABC=45°;
②先根据切线的性质得∠OAP=90°,再证四边形APCO为平行四边形,加上∠AOC=90°,则可判断四边形AOCP为矩形,所以∠PCO=90°,然后根据切线得判断定理得到PC为⊙O的切线;
(2)根据平行四边形的性质得AB∥CD,AD∥BC,再由平行线的性质得∠B+∠A=180°,∠DCE=∠B,由圆内接四边形的性质得∠E+∠A=180°,易得∠DCE=∠E,则根据等腰三角形的判定定理即可得到DC=DE.
解答 (1)解:①连结OA、OC,如图1,
∵OA=OC=4,AC=4$\sqrt{2}$,
∴OA2+OC2=AC2,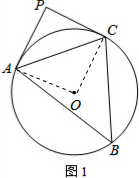
∴△OCA为等腰直角三角形,∠AOC=90°,
∴∠ABC=$\frac{1}{2}$∠AOC=45°;
②直线PC与⊙O相切.理由如下:
∵AP是⊙O的切线,
∴∠OAP=90°,
而∠AOC=90°,
∴AP∥OC,
而AP=OC=4,
∴四边形APCO为平行四边形,
∵∠AOC=90°,
∴四边形AOCP为矩形,
∴∠PCO=90°,
∴PC⊥OC,
∴PC为⊙O的切线;
(2)证明: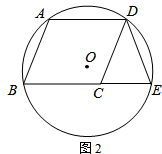 ∵四边形ABCD为平行四边形,
∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠A=180°,∠DCE=∠B,
∵∠E+∠A=180°,
∴∠E=∠B,
∴∠DCE=∠E,
∴DC=DE.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了平行四边形的性质.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | a2×a3=a6 | B. | (a+b)2=a2+b2 | C. | (a+b)(a-b)=a2-b2 | D. | (a2)3=a5 |
4.下列运算正确的是( )
| A. | a3+a3=a6 | B. | 2(a+1)=2a+1 | C. | (-ab)2=a2b2 | D. | a6÷a3=a2 |
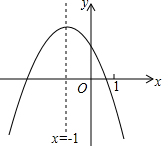 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: