题目内容
6．
如图，在?ABCD中，AE=EB，AF=2，求FC的长．
分析 由四边形ABCD是平行四边形，可证得△AEF∽△CDF，然后由相似三角形的对应边成比例，求得答案．
解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴△AEF∽△CDF，
∴$\frac{AF}{FC}=\frac{AE}{CD}$，
∵AE=EB，
∴AE：CD=AE：AB=1：2，
∵AF=2，
∴FC=4．
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质．注意相似三角形的对应边成比例．
练习册系列答案
相关题目
16．
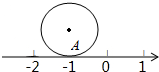如图，圆的直径为1个单位长度，该圆上的点A与数轴上表示-1的点重合，将圆沿数轴滚动1周，点A到达点A′的位置，则点A′表示的数是（ ）
如图，圆的直径为1个单位长度，该圆上的点A与数轴上表示-1的点重合，将圆沿数轴滚动1周，点A到达点A′的位置，则点A′表示的数是（ ）| A． | π-1 | B． | -π-1 | C． | -π-1或π-1 | D． | -π-1或π﹢1 |
17．下列说法正确的是（ ）
| A． | 命题一定是正确的 | B． | 不正确的判断就不是命题 | ||
| C． | 真命题都是公理 | D． | 定理都是真命题 |
16．
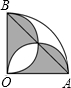如图，半径为1cm，圆心角为90°的扇形OAB中，分别以OA，OB为直径作半圆，则图中阴影部分的面积为（ ）
如图，半径为1cm，圆心角为90°的扇形OAB中，分别以OA，OB为直径作半圆，则图中阴影部分的面积为（ ）| A． | πcm2 | B． | $\frac{2}{3}$πcm2 | C． | $\frac{1}{2}$cm2 | D． | $\frac{2}{3}$cm2 |