题目内容
1.已知$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$,求$\frac{x+y+z}{2x+y-z}$的值.分析 根据比例的性质,可用x表示y,用x表示z,根据分式的性质,可得答案.
解答 解:由$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$,得
y=$\frac{3x}{2}$,z=2x.
$\frac{x+y+z}{2x+y-z}$=$\frac{x+\frac{3x}{2}+2x}{2x+\frac{3x}{2}-2x}$=3.
点评 本题考查了比例的性质,利用比例的性质得出y=$\frac{3x}{2}$,z=2x是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.某校八年级共有四个班,在一次英语测试中四个班的平均分与各班参加考试的人数如表:
则该校八年级参加这次英语测试的所有学生的平均分约为(精确到0.1)( )
| 班级 | 一班 | 二班 | 三班 | 四班 |
| 参加人数 | 51 | 49 | 50 | 60 |
| 班平均分/分 | 83 | 89 | 82 | 79.5 |
| A. | 83.1分 | B. | 83.2分 | C. | 83.4分 | D. | 83.5分 |
10.解方程:①3x2-12=0;②3x2-4x-2=0;③20x2-9x-16=0;④3(4x-1)2=7(4x-1).较简便的解法是( )
| A. | 依次用直接开平方法、配方法、公式法和因式分解法 | |
| B. | ①用直接开平方法,②用公式法,③④用因式分解法 | |
| C. | 依次用因式分解法、公式法、配方法和因式分解法 | |
| D. | ①用直接开平方法,②③用公式法,④用因式分解法 |
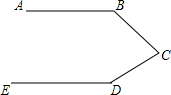 如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件合格.(填“合格”或“不合格”)
如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件合格.(填“合格”或“不合格”) 如图,在?ABCD中,AE=EB,AF=2,求FC的长.
如图,在?ABCD中,AE=EB,AF=2,求FC的长.


