题目内容

3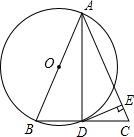．已知：△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E．求证：DE是⊙O的切线．

分析 连接OD，根据圆周角定理得到AD⊥BC，根据等腰三角形的性质得到BD=DC，根据三角形的中位线定理得到OD∥AC，根据平行线的性质得到∠ODE=90°，得到答案．

解答 证明：连接OD，
∵AB为⊙O的直径，
∴AD⊥BC，又AB=AC，
∴BD=DC，
∵BO=OA，
∴OD∥AC，
∴∠ODE=180°-∠AED=90°，
∴DE是⊙O的切线．

点评 本题考查的是切线的判定、等腰三角形的性质，掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键．

练习册系列答案
相关题目
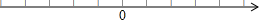13．点A在数轴的原点，另一点B在-3处，A点先向右移动8个单位，再向左移动2个单位到点C处，B点先向左移动1个单位，再向右移动6个单位到点D处．
（1）画出数轴，并在数轴上标出C、D两点的位置；
（2）现有一点P，在数轴上与C、D两点的距离相等，直接写出P点表示的数4．
14．解方程
（1）（x+3）（x-4）=-12
（2）175（x-2）2=28
（3）（20-x）（4x+28）=648．
11．重庆实验外国语学校初2017级学生会进行了爱心义卖活动，准备将义卖获得的利润全部用于易书吧购买图书，免费借阅给全校学生，首次购进的义卖商品单价为25元，共卖出120件，第二次购进的义卖商品的单价是20元，共卖出150件．已知首次义卖的每件售价比第二次多20元，但第二次比第一次少获得600元．
（1）求第二次义卖的商品每件售价是多少元？
（2）为了让全校更多同学借阅到图书，初2017级学生会决定再进行一次义卖活动，此次义卖购进的商品单价为15元，每件售价比第二次上调了a%，则卖出的件数比第二次减少2a%，若第三次获利4500元，求a的值．
18．科学知识是用来为人类服务的，我们应该把它们用于有意义的方面．下面就两个情景请你作出判断：
（1）木工师傅在做完门框后，为防止变形，常常像图中所示的样子钉上两条斜拉的木板条，这样做的数学道理是四边形具有不稳定性，三角形具有稳定性；
（2）在科技创新大赛期间，八年级A班的小强有一个设想，他计划设计一个内角和是2010°的多边形图案，他认为这非常有意义，他的愿望能实现吗？用数学知识说明你的结论．
8．如图，AE∥BD，C是BD上的点，且AB=BC，∠ACD=110°，则∠EAB度数为（　　）
A．70°B．55°C．40°D．35°
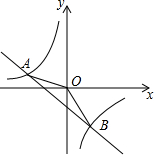15．如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A（-4，2）、B（n，-4）两点．
（1）求上述反比例函数和一次函数的解析式；
（2）求△AOB的面积．
12．先化简，再求值：（3a2-2a-6）-2（2a2-2a-5），其中a=-1．
13．数学活动--“关于三角形全等的条件”
【问题提出】学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
【逐步探究】
（1）第一种情况：当∠B是直角时，如图①，根据HL定理，可得△ABC≌△DEF．
（2）第二种情况：当∠B是钝角时，△ABC≌△DEF仍成立．请你完成证明．
已知：如图②，△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，
求证：△ABC≌△DEF．
（3）第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
【深入思考】
∠B还要满足什么条件，就可以使△ABC≌△DEF？（请直接写出结论．）
在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若∠B≥∠A，则△ABC≌△DEF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网