题目内容
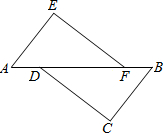 如图,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.求证:
如图,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.求证:(1)△AEF≌△BCD.
(2)∠C=∠E.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据平行线的性质得出∠A=∠B,根据SAS推出△AEF≌△BCD即可;
(2)根据全等三角形的性质得出即可.
(2)根据全等三角形的性质得出即可.
解答:
证明:(1)∵AE∥BC,
∴∠A=∠B,
在△AEF和△BCD中,
,
∴△AEF≌△BCD(SAS);
(2)∵△AEF≌△BCD,
∵∠C=∠E.
∴∠A=∠B,
在△AEF和△BCD中,
|
∴△AEF≌△BCD(SAS);
(2)∵△AEF≌△BCD,
∵∠C=∠E.
点评:本题考查了全等三角形的性质和判定,平行线的性质的应用,解此题的关键是推出△AEF≌△BCD,注意:全等三角形的对应角相等.

练习册系列答案
相关题目
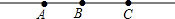 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A、线段AB和线段BA是同一条线段 |
| B、直线AB和直线BA是同一条直线 |
| C、射线BC和射线CB是同一条射线 |
| D、射线AB和射线AC是同一条射线 |
若点A(2a-1,5-a)到两坐标轴的距离相等,则点A的坐标是( )
| A、(3,3) |
| B、(-9,9) |
| C、(3,3)或(-9,9) |
| D、不确定 |
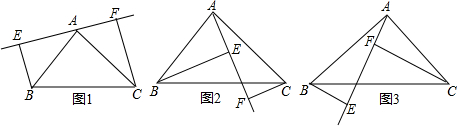
 如下图,∠ABC是平角,过点B作一条射线BD将∠ABC分成∠DBC,∠DBA是什么角时,满足下列要求:
如下图,∠ABC是平角,过点B作一条射线BD将∠ABC分成∠DBC,∠DBA是什么角时,满足下列要求: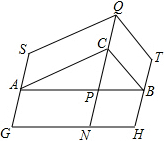 如图,△ABC中,∠ACB=90°,分别以它的三边向外作平行四边形,QC∥GS∥TH交AB于P,交GH于N,且QC=PN,若?ABHG和?SQCA的面积分别为8和6,则?QTBC的面积为
如图,△ABC中,∠ACB=90°,分别以它的三边向外作平行四边形,QC∥GS∥TH交AB于P,交GH于N,且QC=PN,若?ABHG和?SQCA的面积分别为8和6,则?QTBC的面积为 (1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平于EF(
(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平于EF(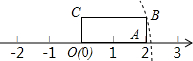 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )