题目内容
对于函数y=x2,下列结论正确的是( )
| A、图象的开口向下 |
| B、y随x增大而增大 |
| C、图象关于y轴对称 |
| D、对于任意实数,都有y>0 |
考点:二次函数的性质
专题:
分析:根据二次函数y=x2的性质进行判断即可;
解答:
解:∵a=1>0,图象的开口向上,对称轴为y轴;
∴当x>0时,y随x的增大而增大,
当x=0时,y=0.
故选C.
∴当x>0时,y随x的增大而增大,
当x=0时,y=0.
故选C.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
直角三角形的两条边分别是6和8,这第三条边的长度是( )
| A、6 | B、8 |
| C、10 | D、以上答案都不对 |
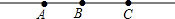 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A、线段AB和线段BA是同一条线段 |
| B、直线AB和直线BA是同一条直线 |
| C、射线BC和射线CB是同一条射线 |
| D、射线AB和射线AC是同一条射线 |
若点A(2a-1,5-a)到两坐标轴的距离相等,则点A的坐标是( )
| A、(3,3) |
| B、(-9,9) |
| C、(3,3)或(-9,9) |
| D、不确定 |
在下面的分式变形中,不正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
在反比例函数y=
(k<0)的图象上有两点,(-1,y1),(-
,y2),则y1-y2的值是( )
| k |
| x |
| 1 |
| 4 |
| A、正数 | B、非正数 |
| C、负数 | D、不能确定 |
 如图,小牛利用全等三角形的知识测量池塘两端A、B的距离,如图△CDO≌△BAO,则只需测出其长度的线段是( )
如图,小牛利用全等三角形的知识测量池塘两端A、B的距离,如图△CDO≌△BAO,则只需测出其长度的线段是( )| A、AO | B、CB | C、BO | D、CD |
 (1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平于EF(
(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平于EF(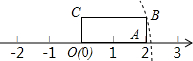 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )