题目内容
 如图所示,△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.
如图所示,△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.(1)请你判断△ABC的形状,并说明理由;
(2)求出最长边AB上的高CD.
考点:勾股定理的逆定理,因式分解的应用,勾股定理
专题:
分析:(1)根据完全平方公式,可得非负数的和为零,可得每个非负数为零,可得a、b的值,然后根据勾股定理逆定理,可得判断△ABC的形状;
(2)利用面积法即可求出最长边AB上的高CD.
(2)利用面积法即可求出最长边AB上的高CD.
解答:
解:(1)∵a2+b2-12a-16b+100=0,
∴(a-6)2+(b-8)2=0,
即:a=6,b=8,
∵a2+b2=62+82=100=102=c2,
∴△ABC的形状为:直角三角形,且∠ACB=90°,AB为最长边;
(2)S△ABC=
AC•BC=
AB•CD,
即ab=c•CD,
∴CD=
=
=4.8.
∴最长边AB上的高CD为4.8.
∴(a-6)2+(b-8)2=0,
即:a=6,b=8,
∵a2+b2=62+82=100=102=c2,
∴△ABC的形状为:直角三角形,且∠ACB=90°,AB为最长边;
(2)S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即ab=c•CD,
∴CD=
| ab |
| c |
| 6×8 |
| 10 |
∴最长边AB上的高CD为4.8.
点评:本题考查了因式分解的应用,利用了非负数的和为零得出a、b的值是解题关键.

练习册系列答案
相关题目
 如图,小牛利用全等三角形的知识测量池塘两端A、B的距离,如图△CDO≌△BAO,则只需测出其长度的线段是( )
如图,小牛利用全等三角形的知识测量池塘两端A、B的距离,如图△CDO≌△BAO,则只需测出其长度的线段是( )| A、AO | B、CB | C、BO | D、CD |
某公司全体员工薪的具体情况如表:
则所有员工年薪的中位数为( )
| 年薪/万元 | 30 | 14 | 9 | 6 | 4 | 3.5 | 3 |
| 员工数/人 | 1 | 1 | 1 | 2 | 7 | 6 | 2 |
| A、9万元 | B、6万元 |
| C、5万元 | D、4万元 |
若
+
有意义,则x应满足的条件是( )
| x-1 |
| 1-x |
| A、x≥1 | B、x≤1 |
| C、x=1 | D、x≠1 |
x3表示( )
| A、3x | B、x+x+x |
| C、x+3 | D、x•x•x |
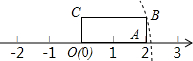 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )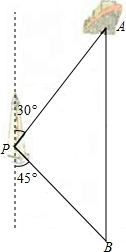 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为