题目内容
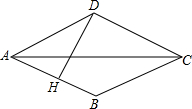 如图,菱形ABCD的边长为15cm,对角线AC=24cm,DH⊥AB于H,则DH的长为( )
如图,菱形ABCD的边长为15cm,对角线AC=24cm,DH⊥AB于H,则DH的长为( )| A、14.4cm |
| B、16.2cm |
| C、15.4cm |
| D、18.2cm |
考点:菱形的性质
专题:
分析:根据菱形的对角线互相垂直平分求出OA,然后利用勾股定理列式求出OB,再根据菱形的面积等于对角线乘积的一半和底乘以高两种方法列式计算即可得解.
解答: 解:连接BD,设AC与BD交于点O,
解:连接BD,设AC与BD交于点O,
∵菱形ABCD对角线AC=24cm,菱形ABCD的边长为15cm,
∴AC⊥BD,AB=15cm,
OA=
AC=
×24=12(cm),
OB=
=9(cm),
则BD=18cm,
菱形ABCD的面积=
AC•BD=AB•DH,
即
×24×18=15×DH,
解得DH=14.4(cm).
故选:A.
 解:连接BD,设AC与BD交于点O,
解:连接BD,设AC与BD交于点O,∵菱形ABCD对角线AC=24cm,菱形ABCD的边长为15cm,
∴AC⊥BD,AB=15cm,
OA=
| 1 |
| 2 |
| 1 |
| 2 |
OB=
| AB2-AO2 |
则BD=18cm,
菱形ABCD的面积=
| 1 |
| 2 |
即
| 1 |
| 2 |
解得DH=14.4(cm).
故选:A.
点评:本题考查了菱形的对角线互相垂直平分的性质,勾股定理的应用,根据菱形的面积的两个求解方法列出方程是解题的关键.

练习册系列答案
相关题目
若
=
,则( )
| x-3 |
| 15-2x |
| A、x=6 | B、x=5 |
| C、x=4 | D、x=3 |
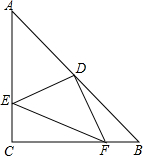 如图,在△ABC中,AC=BC,∠C=90°,D为AB边的中点,点E在AC上,连接DE,过D作DF⊥DE交BC于F.若AE=6cm,BF=2cm,则ED的长为( )
如图,在△ABC中,AC=BC,∠C=90°,D为AB边的中点,点E在AC上,连接DE,过D作DF⊥DE交BC于F.若AE=6cm,BF=2cm,则ED的长为( )A、3
| ||
B、2
| ||
C、3
| ||
D、2
|
 如图,如果张力的位置可表示为(1,3),则王红的位置应表示为( )
如图,如果张力的位置可表示为(1,3),则王红的位置应表示为( )| A、(4,1) |
| B、(4,2) |
| C、(2,4) |
| D、(3,4) |
下列调查中,调查方式选择合理的是( )
| A、为了解旬河水中汞含量是否符合规定标准选择全面调查 |
| B、为了解县师训教研中心36名员工“开展群中国路线教育实践活动”心得体会收交情况选择抽样调查 |
| C、商家为了解某一批“电子白板”的使用寿命选择全面调查 |
| D、为了解空气中PM2.5含量选择抽样调查 |
如图,将一条长为60cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1:2:3,则折痕对应的刻度的可能性有( )


| A、2种 | B、3种 | C、4种 | D、5种 |
在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,则BC的长为( )
| A、8cm | B、7cm |
| C、6cm | D、5cm |
若9a2+6(k-3)a+1是完全平方式,则k的值是( )
| A、±4 | B、±2 | C、3 | D、4或2 |