题目内容
直角坐标系xOy中,有反比例函数y=
(x>0)上的一动点P,以点P为圆心的圆始终与y轴相切,设切点为A
(1)如图1,⊙P运动到与x轴相切时,求OP2的值.
(2)设圆P运动时与x轴相交,交点为B、C,如图2,当四边形ABCP是菱形时,
①求出A、B、C三点的坐标.
②设一抛物线过A、B、C三点,在该抛物线上是否存在点Q,使△QBP的面积是菱形ABCP面积的
?若存在,求出所有满足条件的Q点的坐标;若不存在,说明理由.
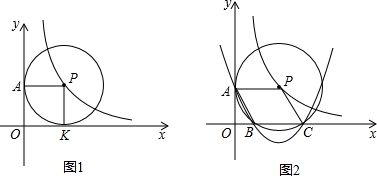
8
| ||
| x |
(1)如图1,⊙P运动到与x轴相切时,求OP2的值.
(2)设圆P运动时与x轴相交,交点为B、C,如图2,当四边形ABCP是菱形时,
①求出A、B、C三点的坐标.
②设一抛物线过A、B、C三点,在该抛物线上是否存在点Q,使△QBP的面积是菱形ABCP面积的
| 1 |
| 2 |
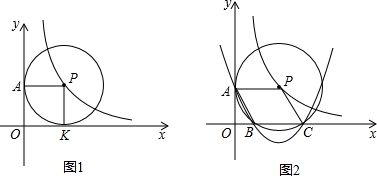
考点:圆的综合题
专题:
分析:(1)当⊙P分别与两坐标轴相切时,PA⊥y轴,PK⊥x轴,x轴⊥y轴,且PA=PK,进而得出PK2,即可得出OP2的值;
(2)①连接PB,设AP=m,过P点向x轴作垂线,垂足为H,则PH=sin60°BP=
m,P(m,
m),进而得出答案;
②求直线PB的解析式,利用过A点或C点且平行于PB的直线解析式与抛物线解析式联立,列方程组求满足条件的Q点坐标即可.
(2)①连接PB,设AP=m,过P点向x轴作垂线,垂足为H,则PH=sin60°BP=
| ||
| 2 |
| ||
| 2 |
②求直线PB的解析式,利用过A点或C点且平行于PB的直线解析式与抛物线解析式联立,列方程组求满足条件的Q点坐标即可.
解答:解:(1)∵⊙P分别与两坐标轴相切,
∴PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵AP=KP,
∴四边形OKPA是正方形,
∴OP2=OK2+PK2=2PK•OK=2xy=2×8
=16
;
(2)①连结BP,
则AP=BP,由于四边形ABCP为菱形,所以AB=BP=AP,△ABP为正三角形,
设AP=m,过P点向x轴作垂线,垂足为H,
则PH=sin60°BP=
m,P(m,
m),
将P点坐标代入到反比例函数解析式中,
则
m2=8
,
解得:m=4,(m=-4舍去),
故P(4,2
),
则AP=4,OA=2
,OB=BH=2,CH=BH=2,
故A(0,2
),B(2,0),C(6,0);

②设过A、B、C三点的抛物线解析式为y=a(x-2)(x-6),
将A点坐标代入得,a=
,
故解析式为y=
x2-
x+2
,
过A点作BP的平行线l抛物线于点Q,则Q点为所求.
设BP所在直线解析式为:y=kx+d,
则
,
解得:
,
故BP所在的直线解析式为:y=
x-2
,
故直线l的解析式为y=
x+2
,直线l与抛物线的交点是方程组
的解,
解得:
,
,
故得Q(0,2
),Q(14,16
),
同理,过C点作BP的平行线交抛物线于点Q1,
则设其解析式为:y=
x+e,则0=6
+e,解得:e=-6
,
故其解析式为:y=
x-6
,
其直线与抛物线的交点是方程组
的解,
可求得Q1(8,2
)和(6,0).
故所求满足条件的Q点有(0,2
),(14,16
),(8,2
)和(6,0).
∴PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵AP=KP,
∴四边形OKPA是正方形,
∴OP2=OK2+PK2=2PK•OK=2xy=2×8
| 3 |
| 3 |
(2)①连结BP,
则AP=BP,由于四边形ABCP为菱形,所以AB=BP=AP,△ABP为正三角形,
设AP=m,过P点向x轴作垂线,垂足为H,
则PH=sin60°BP=
| ||
| 2 |
| ||
| 2 |
将P点坐标代入到反比例函数解析式中,
则
| ||
| 2 |
| 3 |
解得:m=4,(m=-4舍去),
故P(4,2
| 3 |
则AP=4,OA=2
| 3 |
故A(0,2
| 3 |

②设过A、B、C三点的抛物线解析式为y=a(x-2)(x-6),
将A点坐标代入得,a=
| ||
| 6 |
故解析式为y=
| ||
| 6 |
4
| ||
| 3 |
| 3 |
过A点作BP的平行线l抛物线于点Q,则Q点为所求.
设BP所在直线解析式为:y=kx+d,
则
|
解得:
|
故BP所在的直线解析式为:y=
| 3 |
| 3 |
故直线l的解析式为y=
| 3 |
| 3 |
|
解得:
|
|
故得Q(0,2
| 3 |
| 3 |
同理,过C点作BP的平行线交抛物线于点Q1,
则设其解析式为:y=
| 3 |
| 3 |
| 3 |
故其解析式为:y=
| 3 |
| 3 |
其直线与抛物线的交点是方程组
|
可求得Q1(8,2
| 3 |
故所求满足条件的Q点有(0,2
| 3 |
| 3 |
| 3 |
点评:本题考查了二次函数的综合运用以及二元二次方程组解法和正方形的判定以及菱形的性质等知识,关键是由菱形、圆的性质,数形结合解题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 AB、AC、BC是三角形形状公园的示意图,现准备在公园内修建一座亭子,使得亭子到三条小路的距离相等,你能找到亭子应该修建的位置吗?若以亭子为中心修建一条圆形的道路,并且使这条圆形的道路与公园外围的三条小路都相切,你能将这条圆形小路画出来吗?(保留作图痕迹,不要求写出作法)
AB、AC、BC是三角形形状公园的示意图,现准备在公园内修建一座亭子,使得亭子到三条小路的距离相等,你能找到亭子应该修建的位置吗?若以亭子为中心修建一条圆形的道路,并且使这条圆形的道路与公园外围的三条小路都相切,你能将这条圆形小路画出来吗?(保留作图痕迹,不要求写出作法) 由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:
由于被墨水污染,一道几何题仅能见到如图所示的图形和文字: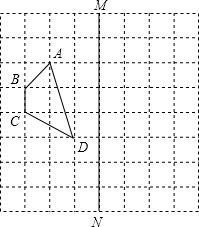 如图,在正方形网络上有一个四边形ABCD.
如图,在正方形网络上有一个四边形ABCD.