Question

10．如图，AB是⊙O的直径，PA、PC分别切⊙O于点A、C，延长PC交AB的延长线于点D，DE⊥PO交PO的延长线于点E．若PC=6，sin∠PDA=$\frac{3}{5}$．
求：（1）OA的长；
（2）tan∠ODE的值．

Answer 1

分析 （1）连接OC，由切线长定理可知PA=PC=6，由sin∠PDA=$\frac{3}{5}$可求得PD=10，AD=8，设OC=x，则OD=8-x，CD=4，在Rt△DOC中由勾股定理可求得OC的长，从而得到OA的长；
（2）先证明∠ODE=∠APO，然后根据PA和AO的长可求得tan∠ODE的值．

解答 解：（1）如图所示：连接OC．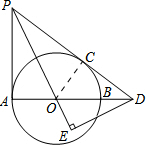

∵AB是圆O的直径，∠PAB=90°，
∴PA是圆O的切线．
∵PD是圆O的切线，
∴PA=PC=6，OC⊥PD．
∵sin∠PDA=$\frac{3}{5}$，
∴$\frac{PA}{PD}=\frac{3}{5}$，即$\frac{6}{PD}=\frac{3}{5}$．
∴PD=10．
∴CD=10-6=4．
∴AD=10×$\frac{4}{5}$=8．
设OC=x，则OD=8-x，在Rt△DOC中由勾股定理得：x²+4²=（8-x）²，
解得：x=3．
∴OA=3．
（2）∵在△POA和△DOE中，∠AOP=∠EOD，∠E=∠A，
∴∠ODE=∠OPA．
∴tan∠ODE=$\frac{OA}{PA}=\frac{3}{6}=\frac{1}{2}$．

点评 本题主要考查的是切线的性质、切线长定理、勾股定理、锐角三角函数的定义，在Rt△DOC中由勾股定理得到关于x的方程是解题的关键．