题目内容
1. 如图,直线y1=kx(k>0)与双曲线y2=$\frac{4}{x}$交于A(m1,n1)、B(m2,n2)两点.
如图,直线y1=kx(k>0)与双曲线y2=$\frac{4}{x}$交于A(m1,n1)、B(m2,n2)两点.(1)观察图象,比较当x<0时,y1与y2的大小;
(2)求m1n2+m2n1的值.
分析 (1)根据图象即可求得;
(2)根据题意可知A、B关于原点对称,所以m1=-m2,n1=-n2,由反比例函数相似系数k的几何意义得出m1n1,=4,m2n2=4,进而得出m1n1,=-m1n2=4,m2n2=-m2n1=4,即可求得m1n2+m2n1=-8.
解答 解:(1)由图象可知,当m2<x<0时,y1>y2;当x<m2时,y1<y2;
(2)∵直线y1=kx(k>0)与双曲线y2=$\frac{4}{x}$交于A(m1,n1)、B(m2,n2)两点.
∴m1=-m2,n1=-n2,
∵A(m1,n1)、B(m2,n2)是双曲线y2=$\frac{4}{x}$上的点,
∴m1n1,=4,m2n2=4,
∴m1n1,=-m1n2=4,m2n2=-m2n1=4
∴m1n2+m2n1=-8.
点评 本题考查了反比例函数和一次函数的交点问题,解题的关键是得出m1n1,=-m1n2=4,m2n2=-m2n1=4.

练习册系列答案
相关题目
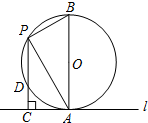 如图,已知半径为4的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(4<x<8)
如图,已知半径为4的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(4<x<8) 如图,AB是⊙O的直径,PA、PC分别切⊙O于点A、C,延长PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.若PC=6,sin∠PDA=$\frac{3}{5}$.
如图,AB是⊙O的直径,PA、PC分别切⊙O于点A、C,延长PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.若PC=6,sin∠PDA=$\frac{3}{5}$.