Question

8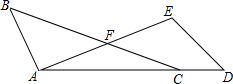．如图，点A，C，D在同一条直线上，BC与AE交于点F，FA=FC，∠D=
∠B，AD=BC．
（1）求证：△ABC≌△EDA；
（2）尺规作图：作△AED沿着AD方向平移AC长度后的三角形；（保留作图痕迹，不写作法）
（3）若AC=5cm，∠EAD=20°，请问△AED经过怎样的运动变为
△CAB？

Answer 1

分析 （1）利用两角以及夹边对应相等的两个三角形全等来判断即可．
（2）根据要求画出图形即可．
（3）利用平移和旋转即可解决问题．

解答 解：（1）∵FA=FC，
∴∠FAC=∠FCA，
在△ABC和△EDA中，
$\left\{\begin{array}{l}{∠ACB=∠EAD}\\{BC=AD}\\{∠B=∠D}\end{array}\right.$，
∴△ABC≌△EDA．
（2）如图所示．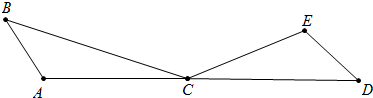

（3）△AED先向右平移5cm，再绕点C逆时针旋转160°就可以与△ABC重合．

点评 本题考查全等三角形的判定和性质、平移以及旋转的有关知识，解题的关键是灵活掌握全等三角形的判定方法，利用平移以及旋转解决图形变换问题，属于中考常考题型．