题目内容
19.a为何值时,关于x的方程$\frac{2}{x-2}$+$\frac{ax}{{x}^{2}-4}$=$\frac{3}{x+2}$无解?分析 分式方程去分母转化为整式方程,由分式方程无解确定出a的值即可.
解答 解:由原方程得:2(x+2)+ax=3(x-2),
整理得:(a-1)x=-10,
(i)当a-1=0,即a=1时,原方程无解;
(ii)当a-1≠0,原方程有增根x=±2,
当x=2时,2(a-1)=-10,即a=-4;
当x=-2时,-2(a-1)=-10,即a=6,
即当a=1,-4或6时原方程无解.
点评 此题考查了分式方程的解,熟练掌握分式方程无解的条件是解本题的关键.

练习册系列答案
相关题目
14.整式:-0.34x2y,π,$\frac{a+1}{2}$,-52xyz2,$\frac{1}{3}$x2-$\frac{1}{5}$y,-$\frac{1}{3}$xy2-$\frac{1}{2}$中,单项式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.下列运算中,计算正确的是( )
| A. | a3•a6=a9 | B. | (a2)3=a5 | C. | 4a3-2a2=2 | D. | (3a)2=6a2 |
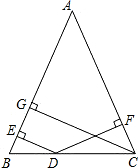 如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.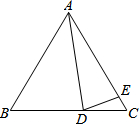 在△ABC中,AB=AC,∠BAD=40°,AE=AD,求∠EDC的度数.
在△ABC中,AB=AC,∠BAD=40°,AE=AD,求∠EDC的度数. 如图所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是AD∥CF,AD=CF=BE.
如图所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是AD∥CF,AD=CF=BE. 如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.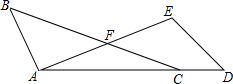 如图,点A,C,D在同一条直线上,BC与AE交于点F,FA=FC,∠D=
如图,点A,C,D在同一条直线上,BC与AE交于点F,FA=FC,∠D=