题目内容
2.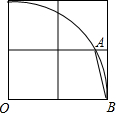 如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为2+$\sqrt{3}$.
如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为2+$\sqrt{3}$.
分析 连接OA,过点A作AC⊥OB于点C,由题意知AC=1、OA=OB=2,从而得出OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{3}$、BC=OB-OC=2-$\sqrt{3}$,在Rt△ABC中,根据tan∠ABO=$\frac{AC}{BC}$可得答案.
解答 解:如图,连接OA,过点A作AC⊥OB于点C,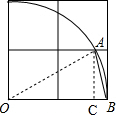
则AC=1,OA=OB=2,
∵在Rt△AOC中,OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴BC=OB-OC=2-$\sqrt{3}$,
∴在Rt△ABC中,tan∠ABO=$\frac{AC}{BC}$=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$.
故答案是:2+$\sqrt{3}$.
点评 本题主要考查解直角三角形,根据题意构建一个以∠ABO为内角的直角三角形是解题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
13.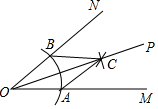 如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )
如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )
 如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )
如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
7. 如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是( )
如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是( )
 如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是( )
如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是( )| A. | O1 | B. | O2 | C. | O3 | D. | O4 |
14.在数学活动课上,同学们用木条做成一个四边形框架,要判断该四边形是否为菱形,下列测量方案可行的是( )
| A. | 测量该四边形的对角线是否互相垂直 | |
| B. | 测量该四边形的对角线是否相等 | |
| C. | 测量该四边形的对角线是否互相平分 | |
| D. | 测量该四边形的四条边是否都相等 |
11.直角坐标系中,点P(x,y)在第二象限,且P到x轴、y轴距离分别为3,7,则P点坐标为( )
| A. | (-3,7) | B. | (-7,3) | C. | (3,7) | D. | (7,3) |
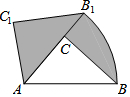 如图,在△ACB中,∠BAC=50°,AC=4,AB=6.现将△ACB绕点A逆时针旋转50°得到△AC1B1则阴影部分的面积为5π.
如图,在△ACB中,∠BAC=50°,AC=4,AB=6.现将△ACB绕点A逆时针旋转50°得到△AC1B1则阴影部分的面积为5π. 如图,所示的几何体是由若干个大小相同的小正方体组成的,则该几何体的左视图(从左面看)是( )
如图,所示的几何体是由若干个大小相同的小正方体组成的,则该几何体的左视图(从左面看)是( )



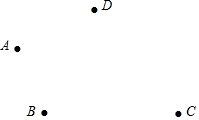 如图,平面上有四个点A,B,C,D,按照以下要求完成问题:
如图,平面上有四个点A,B,C,D,按照以下要求完成问题: