题目内容
12.计算或化简(1)$\frac{\sqrt{20}+\sqrt{5}}{\sqrt{45}}$-$\sqrt{\frac{1}{3}}$•$\sqrt{6}$
(2)(π-1)0+${(-\frac{1}{2})}^{-1}$+|5-$\sqrt{27}$|-2$\sqrt{3}$.
分析 (1)先把$\sqrt{20}$和$\sqrt{45}$为最简二次根式,然后根据二次根式的乘除法则运算;
(2)根据零指数幂、负整数指数幂和绝对值的意义计算.
解答 解:(1)原式=$\frac{2\sqrt{5}+\sqrt{5}}{3\sqrt{5}}$-$\sqrt{\frac{1}{3}×6}$
=1-$\sqrt{2}$;
(2)原式=1-2+3$\sqrt{3}$-5-2$\sqrt{3}$
=$\sqrt{3}$-6.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
4.把弯曲的道路改直,就能缩短路程,其中蕴含的数学原理是( )
| A. | 过一点有无数条直线 | B. | 两点确定一条直线 | ||
| C. | 两点之间线段最短 | D. | 线段是直线的一部分 |
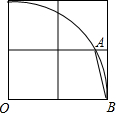 如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为2+$\sqrt{3}$.
如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为2+$\sqrt{3}$.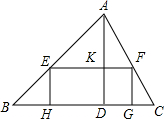 在锐角△ABC中,边BC长为18,高AD长为12
在锐角△ABC中,边BC长为18,高AD长为12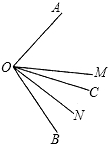 如图,OM是∠AOB的平分线,射线OC在∠BOM的内部,ON是∠BOC的平分线,若∠AOC=60°,求∠MON的大小.
如图,OM是∠AOB的平分线,射线OC在∠BOM的内部,ON是∠BOC的平分线,若∠AOC=60°,求∠MON的大小.