题目内容
17.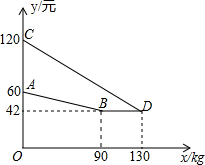 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.(1)求线段AB所表示的y1与x之间的函数表达式;线段CD所表示的y2与x之间的函数表达式.
(2)当该产品产量为多少时,获得的利润最大?最大利润是多少?
分析 (1)根据线段AB、线段CD经过的两点的坐标利用待定系数法确定一次函数的表达式即可;
(3)利用:总利润=每千克利润×产量,根据x的取值范围列出有关x的二次函数,求得最值比较可得.
解答 解:(1)设线段AB所表示的y1与x之间的函数关系式为y1=k1x+b1,
∵y1=k1x+b1的图象过点(0,60)与(90,42),
∴$\left\{\begin{array}{l}{{b}_{1}=60}\\{90{k}_{1}+{b}_{1}=42}\end{array}\right.$
∴$\left\{\begin{array}{l}{{k}_{1}=-0.2}\\{{b}_{1}=60}\end{array}\right.$,
∴段AB所表示的一次函数的表达式为;y1=-0.2x+60(0≤x≤90);
设y2与x之间的函数关系式为y2=k2x+b2,
∵经过点(0,120)与(130,42),
∴$\left\{\begin{array}{l}{{b}_{2}=120}\\{130{k}_{2}+{b}_{2}=42}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=-0.6}\\{{b}_{2}=120}\end{array}\right.$,
∴线段CD所表示的一次函数的表达式为y2=-0.6x+120(0≤x≤130);
(2)设产量为xkg时,获得的利润为W元,
①当0≤x≤90时,W=x[(-0.6x+120)-(-0.2x+60)]=-0.4(x-75)2+2250,
∴当x=75时,W的值最大,最大值为2250;
②当90≤x≤130时,W=x[(-0.6x+120)-42]=-0.6(x-65)2+2535,
∴当x=90时,W=-0.6(90-65)2+2535=2160,
由-0.6<0知,当x>65时,W随x的增大而减小,
∴90≤x≤130时,W≤2160,
因此当该产品产量为75kg时,获得的利润最大,最大值为2250.
点评 本题考查了待定系数法求函数解析式及二次函数的应用,解题的关键是从实际问题中抽象出二次函数模型.

 小题狂做系列答案
小题狂做系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{2}{3}$$\sqrt{3}$ |
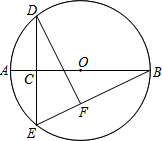 已知:⊙O的半径为5,点C在直径AB上,过点C作⊙O的弦DE⊥AB,过点D作直线 EB的垂线DF,垂足为点F,设AC=x,EF=y.
已知:⊙O的半径为5,点C在直径AB上,过点C作⊙O的弦DE⊥AB,过点D作直线 EB的垂线DF,垂足为点F,设AC=x,EF=y.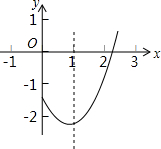 在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是-1<x2<0.
在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是-1<x2<0.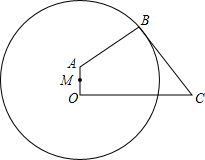 如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.
如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.