题目内容
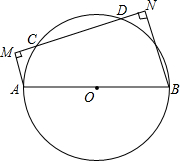 AB为⊙O的直径,CD为弦,AM⊥CD于M,BN⊥CD于N.
AB为⊙O的直径,CD为弦,AM⊥CD于M,BN⊥CD于N.(1)求证:CM=DN;
(2)若AB=10,CD=8,求BN+AM的值.
考点:垂径定理,勾股定理,梯形中位线定理
专题:
分析:(1)过点O作OE⊥MN于点E,根据垂径定理可知CE=DE,再根据AM⊥CD于M,BN⊥CD于N可知AM∥OE∥BN,由点O是AB的中点可知,OE是梯形ABNM的中位线,故ME=NE,由此可得出结论;
(2)连接OC,根据勾股定理可得出OE的长,再根据(1)中OE是梯形ABNM的中位线即可得出结论.
(2)连接OC,根据勾股定理可得出OE的长,再根据(1)中OE是梯形ABNM的中位线即可得出结论.
解答: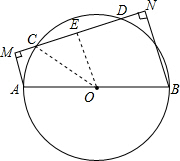 (1)证明:过点O作OE⊥MN于点E,
(1)证明:过点O作OE⊥MN于点E,
∵OE⊥MN,
∴CE=DE.
∵AM⊥CD于M,BN⊥CD于N,
∴AM∥OE∥BN,
∵点O是AB的中点,
∴OE是梯形ABNM的中位线,
∴ME=NE,
∴ME-CE=NE-DE,即CM=DN;
(2)连接OC,
∵AB=10,
∴OC=5.
∵OE⊥MN,CD=8,
∴CE=4,
∴OE=
=
=3,
∵由(1)知OE是梯形ABNM的中位线,
∴BN+AM=2OE=6.
 (1)证明:过点O作OE⊥MN于点E,
(1)证明:过点O作OE⊥MN于点E,∵OE⊥MN,
∴CE=DE.
∵AM⊥CD于M,BN⊥CD于N,
∴AM∥OE∥BN,
∵点O是AB的中点,
∴OE是梯形ABNM的中位线,
∴ME=NE,
∴ME-CE=NE-DE,即CM=DN;
(2)连接OC,
∵AB=10,
∴OC=5.
∵OE⊥MN,CD=8,
∴CE=4,
∴OE=
| OC2-CE2 |
| 52-42 |
∵由(1)知OE是梯形ABNM的中位线,
∴BN+AM=2OE=6.
点评:本题考查的是垂径定理即勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,∠CAB=∠CBD,AB=4,CB=5,AC=6,BD=7.5.求CD的长.
如图,∠CAB=∠CBD,AB=4,CB=5,AC=6,BD=7.5.求CD的长.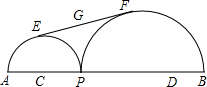 已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别以AP和BP为直径作半圆,点E,F分别为以AP和BP为直径所作半圆的弧的中点,连接EF,点G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为
已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别以AP和BP为直径作半圆,点E,F分别为以AP和BP为直径所作半圆的弧的中点,连接EF,点G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为 如图,在△ABC中,∠B=45°,∠C=30°,D是AC中点,DE⊥BC,求
如图,在△ABC中,∠B=45°,∠C=30°,D是AC中点,DE⊥BC,求