题目内容
6.计算:$\sqrt{\frac{25}{2}}$-$\sqrt{32}$+$\sqrt{18}$.分析 首先化简二次根式,进而合并同类二次根式得出答案.
解答 解:原式=$\frac{5\sqrt{2}}{2}$-4$\sqrt{2}$+3$\sqrt{2}$
=$\frac{3\sqrt{2}}{2}$.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
18.下列各式中,不能用平方差公式计算的是( )
| A. | (2x-y)(2x+y) | B. | (-x+y)(x-y) | C. | (b-a)(b+a) | D. | (x-y)(-y-x) |
15.若式子$\frac{x-3}{\sqrt{x-1}-1}$有意义,则x的取值范围是( )
| A. | x≥1且x≠2 | B. | x≥1 | C. | x>1且x≠2且x≠3 | D. | x>1且x≠2 |
16.下列语句正确的是( )
| A. | 如果一个数的立方根是这个数本身,那么这个数一定是0 | |
| B. | 一个数的立方根不是正数就是负数 | |
| C. | 负数没有立方根 | |
| D. | 一个不为零的数的立方根和这个数同号,0的立方根是0 |
 如图,已知MN⊥AB于P,MN⊥CD于Q,∠2=70°,求∠1.
如图,已知MN⊥AB于P,MN⊥CD于Q,∠2=70°,求∠1.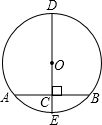 如图,DE是⊙O的直径,弦AB⊥DE,垂足为C,若AB=8,OC=3.求⊙O的半径.
如图,DE是⊙O的直径,弦AB⊥DE,垂足为C,若AB=8,OC=3.求⊙O的半径.