题目内容
8.直线y=-x+2与x轴交于点A,与y轴交于点B,O是原点,点P是线段AB上的动点(包括A、B两点),以OP为直径作⊙Q,则⊙Q的面积不可能是( )| A. | 1.5π | B. | π | C. | $\frac{3}{4}$π | D. | $\frac{1}{2}$π |
分析 求出OA、OB,AB,根据面积公式求出高OC,即可求最大圆的面积和最小圆的面积,即可得出选项.
解答 解:如图: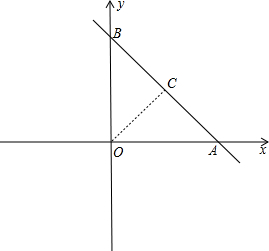
∵直线y=-x+2与x轴交于点A,与y轴交于点B,
∴OA=OB=2,
由勾股定理得:AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$
过O作OC⊥AB于C,则O到直线AB的最短距离是OC的长,
由三角形面积公式得:$\frac{1}{2}$×OB×OA=$\frac{1}{2}×$AB×OC,
解得:OC=$\sqrt{2}$,
当P和C点重合时,⊙Q的面积最小,是π×($\frac{1}{2}$$\sqrt{2}$)2=$\frac{1}{2}$π,
当P和A或B重合时,⊙Q的面积最大,是π×12=π,
即$\frac{1}{2}$π≤⊙Q的面积≤π,
故选A.
点评 本题考查了坐标与图形性质,勾股定理,三角形的面积的应用,能求出最大圆和最小圆的面积是解此题的关键.

练习册系列答案
相关题目
3. 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )| A. | ∠ACD=120° | B. | ∠ACD=∠BCE | C. | ∠ACE=120° | D. | ∠ACE-∠BCD=120° |
13.下列结论错误的是( )
| A. | 若a=b,则a-c=b-c | B. | 若a=b,则ax=bx | C. | 若x=2,则x2=2x | D. | 若ax=bx,则a=b |
17.书店、学校、食堂在平面上分别用A、B、C来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC的度数应该是( )
| A. | 65° | B. | 35° | C. | 165° | D. | 135° |
 如图,在△ABC中,AB>AC,在边AB上,取点D,在AC上取点E,使AD=AE,直线DE和BC的延长线交于点P.
如图,在△ABC中,AB>AC,在边AB上,取点D,在AC上取点E,使AD=AE,直线DE和BC的延长线交于点P. 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.