题目内容
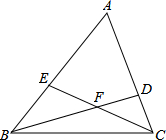已知△ABC，D在AC上，AD：DC=2：1，能否在AB上找到一点E，使得线段EC的中点在BD上．考点：平行线分线段成比例
专题：
分析：过E作EM∥BD，交AC于M，根据平行线分线段成比例定理求出AM=DM=CD，再根据平行线分线段成比例定理求出F为EC中点即可．
解答：解：在AB上能找到一点E，使得线段EC的中点在BD上，
当E为AB中点时，线段EC的中点在BD上，
理由是：过E作EM∥BD，交AC于M，
∵AE=BE，
∴AM=DM，
∵AD：DC=2：1，
∴CD=DM=AM，
∵BD∥EM，
∴EF=CF，
即F为EC的中点，
即在AB上能找到一点E，使得线段EC的中点在BD上．
当E为AB中点时，线段EC的中点在BD上，
理由是：过E作EM∥BD，交AC于M，
∵AE=BE，
∴AM=DM，
∵AD：DC=2：1，
∴CD=DM=AM，
∵BD∥EM，
∴EF=CF，
即F为EC的中点，
即在AB上能找到一点E，使得线段EC的中点在BD上．
点评：本题考查了平行线分线段成比例定理的应用，主要考查学生的推理能力，题目比较好，难度适中．
练习册系列答案
智慧小复习系列答案
相关题目
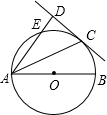如图，已知AB是⊙O的直径，点E为⊙O上一点，且AC平分∠BAE交⊙O于C，过C作CD⊥AE，垂足为D．
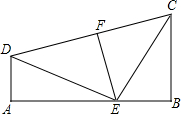已知：如图，AD⊥AB于点A，BC⊥AB于点B．E是AB上一点，DE⊥CE，AE=BC．EF是△DEC的中线．求证：EF是CD的垂直平分线．
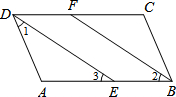推理填空题．