题目内容
10.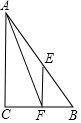 如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )
如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )| A. | △ABC是直角三角形 | B. | AF是△ABC的中位线 | ||
| C. | EF是△ABC的中位线 | D. | △BEF的周长为6 |
分析 根据勾股定理等逆定理、三角形的中位线的性质,一一判断即可.
解答 解:A、正确.∵AB=5,BC=3,AC=4,
∴AB2=BC2+AC2,
∴△ACB是直角三角形,故正确.
B、错误.AF是△ABC的中线,不是中位线.
C、正确.∵点E,F分别是AB,BC的中点,
∴EF是△ABC的中位线,故正确.
D、正确.易知EF=$\frac{1}{2}$AC=2,EB=$\frac{1}{2}$AB=$\frac{5}{2}$,FB=$\frac{1}{2}$BC=$\frac{3}{2}$,
∴△EFB的周长=6,故正确,
故选B.
点评 本题考查三角形的中位线定理、勾股定理的逆定理等知识,解题的关键是灵活运用所学知识解决问题,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
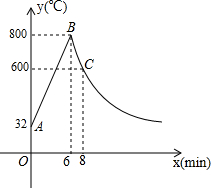 如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.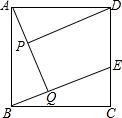 已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.求证:AP=BQ.
已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.求证:AP=BQ.