题目内容
2．
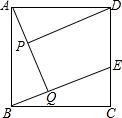已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．求证：AP=BQ．
分析 根据正方形的性质得出AD=BA，∠BAQ=∠ADP，再根据已知条件得到∠AQB=∠DPA，判定△AQB≌△DPA并得出结论；
解答 证明：∵正方形ABCD
∴AD=BA，∠BAD=90°，即∠BAQ+∠DAP=90°
∵DP⊥AQ
∴∠ADP+∠DAP=90°
∴∠BAQ=∠ADP
∵AQ⊥BE于点Q，DP⊥AQ于点P
∴∠AQB=∠DPA=90°
∴△AQB≌△DPA（AAS）
∴AP=BQ
点评 本题主要考查了正方形以及全等三角形，解决问题的关键是掌握：正方形的四条边相等，四个角都是直角．解题时需要运用：有两角和其中一角的对边对应相等的两个三角形全等，以及全等三角形的对应边相等．
练习册系列答案
相关题目
10．
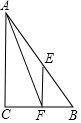如图，在△ABC中，AB=5，BC=3，AC=4，点E，F分别是AB，BC的中点．以下结论错误的是（ ）
如图，在△ABC中，AB=5，BC=3，AC=4，点E，F分别是AB，BC的中点．以下结论错误的是（ ）| A． | △ABC是直角三角形 | B． | AF是△ABC的中位线 | ||
| C． | EF是△ABC的中位线 | D． | △BEF的周长为6 |
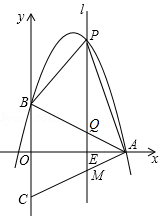如图，在等腰△ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=ax2+$\frac{7}{2}$x+c经过A（8，0）、B（0，4）两点．