题目内容
7. 如图所示,点E为其内部任意一点,∠BED=∠B+∠D,求证:AB∥CD.
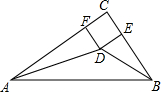
如图所示,点E为其内部任意一点,∠BED=∠B+∠D,求证:AB∥CD.
分析 过点E作EF∥AB,如图,根据平行线的性质得∠1=∠B,由于∠1+∠2=∠B+∠D,则∠2=∠D,于是可判断EF∥CD,然后根据两条直线都和第三条直线平行,那么这两条直线平行即可得到结论.
解答 证明:过点E作EF∥AB,如图,
∵EF∥AB,
∴∠1=∠B,
∵∠BED=∠B+∠D,即∠1+∠2=∠B+∠D,
∴∠2=∠D,
∴EF∥CD,
而EF∥AB,
∴AB∥CD.
点评 本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.

练习册系列答案
相关题目
17.因式分解3y2-6y+3,结果正确的是( )
| A. | 3(y-1)2 | B. | 3(y2-2y+1) | C. | (3y-3)2 | D. | $\sqrt{3}(y-1)^{2}$ |
18.-3的绝对值等于( )
| A. | -3 | B. | 3 | C. | ±3 | D. | $\sqrt{3}$ |

 如图,已知在△ABC中,∠ACB=90°,∠CAB和∠ABC的平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:四边形CEDF正方形.
如图,已知在△ABC中,∠ACB=90°,∠CAB和∠ABC的平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:四边形CEDF正方形.